题目内容
定义两种运算:a⊕b=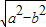 ,a?b=
,a?b=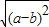 ,则函数f(x)=
,则函数f(x)=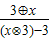 为( )
为( )A.偶函数
B.奇函数
C.奇函数且为偶函数
D.非奇函数且非偶函数
【答案】分析:利用条件先化简f(x),然后利用函数奇偶性的定义进行判断.
解答:解:由定义可知3⊕x=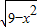 ,x?3=
,x?3=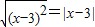 ,
,
所以f(x)=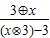 =
=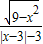 ,
,
要使函数有意义,则9-x2≥0,解得-3≤x≤3,
所以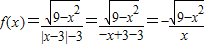 ,
,
所以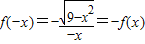 ,所以函数f(x)为奇函数.
,所以函数f(x)为奇函数.
故选B.
点评:本题主要考查新定义的应用,函数奇偶性的应用,利用函数的定义域将函数进行化简是解决本题的关键.综合性较强.
解答:解:由定义可知3⊕x=
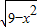 ,x?3=
,x?3=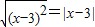 ,
,所以f(x)=
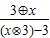 =
=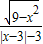 ,
,要使函数有意义,则9-x2≥0,解得-3≤x≤3,
所以
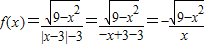 ,
,所以
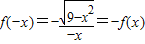 ,所以函数f(x)为奇函数.
,所以函数f(x)为奇函数.故选B.
点评:本题主要考查新定义的应用,函数奇偶性的应用,利用函数的定义域将函数进行化简是解决本题的关键.综合性较强.

练习册系列答案
相关题目
定义两种运算:a⊕b=a2+b2,a⊙b=ab(a,b∈R),则函数f(x)=
是( )
| 2⊙x |
| (x⊕2)-2 |
| A、奇函数 |
| B、偶函数 |
| C、既是奇数又是偶函数 |
| D、既不是奇函数也不是偶函数 |