题目内容
 (2010•汕头模拟)在实验中一粒石子落入右图阴影部分的概率是
(2010•汕头模拟)在实验中一粒石子落入右图阴影部分的概率是1-
| π |
| 8 |
1-
.| π |
| 8 |
分析:可先矩形的面积S,而空白部分的两半圆的直径为2,面积之和A可求则,阴影部分的面积S-A,记“实验中一粒石子落入右图阴影部分”为事件B,由几何概率的计算公式可得P(B)=1-
,从而可求
| A |
| S |
解答:解:如图所示矩形的面积S=4×2=8
空白部分的两半圆的直径为2,面积之和A=π,阴影部分的面积S-A=8-π
记“实验中一粒石子落入右图阴影部分”为事件B,由几何概率的计算公式可得P(B)=1-
=
=1-
故答案为:1-
空白部分的两半圆的直径为2,面积之和A=π,阴影部分的面积S-A=8-π
记“实验中一粒石子落入右图阴影部分”为事件B,由几何概率的计算公式可得P(B)=1-
| A |
| S |
| 8-π |
| 8 |
| π |
| 8 |
故答案为:1-
| π |
| 8 |
点评:本题主要考查了与面积有关的几何概率公式的应用,解题中的关键是要分别求出矩形及阴影部分的面积,属于公式的简单应用.

练习册系列答案
相关题目
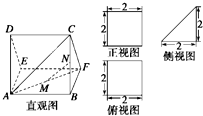 (2010•汕头模拟)如图,多面体AEDBFC的直观图及三视图如图所示,M,N分别为AF,BC的中点.
(2010•汕头模拟)如图,多面体AEDBFC的直观图及三视图如图所示,M,N分别为AF,BC的中点. (2010•汕头模拟)如图,在四边形ABCD中,设
(2010•汕头模拟)如图,在四边形ABCD中,设