题目内容
（2010•汕头模拟）已知函数f（x）=ax2+bx+3a+b是偶函数，定义域为[a-1，2a]，则f（
）=
．
| 1 |
| 2 |
| 13 |
| 12 |
| 13 |
| 12 |
分析：根据函数的奇偶性与定义域，可以求出a，b的值，得到函数的解析式，再把x=
代入解析式，就可求出f（
）=的值．
| 1 |
| 2 |
| 1 |
| 2 |
解答：解：∵函数f（x）=ax2+bx+3a+b是偶函数，∴f（-x）=f（x），
即ax2-bx+3a+b=ax2+bx+3a+b恒成立，
∴b=0
又∵函数的定义域为[a-1，2a]，
∴a-1=-2a，
∴a=
∴f（x）=
x2+1，
∴f（
）=
故答案为
即ax2-bx+3a+b=ax2+bx+3a+b恒成立，
∴b=0
又∵函数的定义域为[a-1，2a]，
∴a-1=-2a，
∴a=
| 1 |
| 3 |
∴f（x）=
| 1 |
| 3 |
∴f（
| 1 |
| 2 |
| 13 |
| 12 |
故答案为
| 13 |
| 12 |
点评：本题主要考查函数奇偶性的定义，以及函数值的求法，属于基础题．
练习册系列答案
轻松暑假总复习系列答案
相关题目
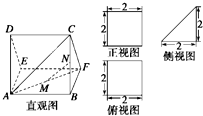（2010•汕头模拟）如图，多面体AEDBFC的直观图及三视图如图所示，M，N分别为AF，BC的中点．
（2010•汕头模拟）如图，在四边形ABCD中，设