题目内容
已知A,B,C不共线,
+2
+3
=
,则∠AOB、∠BOC、∠COA中( )
| OA |
| OB |
| OC |
| 0 |
| A、至少有一个是锐角 |
| B、至少有两个是钝角 |
| C、至多有一个是钝角 |
| D、三个都是钝角 |
分析:设
=
,
=
,
=
,假设
•
>0,则
•
<0,
•
<0,
可得∠BOC 和∠COA 为钝角.
| OA |
| a |
| OB |
| b |
| OC |
| c |
| a |
| b |
| OB |
| OC |
| OA |
| OC |
可得∠BOC 和∠COA 为钝角.
解答:解:设
=
,
=
,
=
.∵
+2
+3
=
,
=-
-
,
假设
•
>0,即∠AOB为锐角,则
•
=|
|•|
|•cos∠BOC=
•(-
-
)=
-
•
-
2<0,∴cos∠BOC<0,∠BOC 为钝角.
∵
•
=|
|•|
|•cos∠COA=
•(-
-
)=-
-
•
<0,∴cos∠COA<0,
∴∠COA 为钝角.
故选 B.
| OA |
| a |
| OB |
| b |
| OC |
| c |
| OA |
| OB |
| OC |
| 0 |
| c |
| ||
| 3 |
| 2 |
| 3 |
| b |
假设
| a |
| b |
| OB |
| OC |
| OB |
| OC |
| b |
| ||
| 3 |
| 2 |
| 3 |
| b |
-
| 1 |
| 3 |
| a |
| b |
| 2 |
| 3 |
| b |
∵
| OA |
| OC |
| OA |
| OC |
| a |
| ||
| 3 |
| 2 |
| 3 |
| b |
| ||
| 3 |
| 2 |
| 3 |
| a |
| b |
∴∠COA 为钝角.
故选 B.
点评:本题考查本题考查两个向量的数量积的定义,数量积公式的应用.

练习册系列答案
相关题目
 ,则∠AOB、∠BOC、∠COA中
,则∠AOB、∠BOC、∠COA中 ,则∠AOB、∠BOC、∠COA中( )
,则∠AOB、∠BOC、∠COA中( )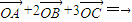 ,则∠AOB、∠BOC、∠COA中( )
,则∠AOB、∠BOC、∠COA中( )