��Ŀ����
����Ŀ����ij���������ŵ������У������ȡ100��Ŀ�������ָ���ļ�����������
��������ָ��t | ��0��50] | ��50��100] | ��100��150] | ��150��200�� | ��200��300] | ��300��+�ޣ� |
�����ȼ� | �� | �� | ����Ⱦ | �����Ⱦ | �ж���Ⱦ | ������Ⱦ |
����K | 5 | 23 | 22 | 25 | 15 | 10 |
��1�����ó��и�ҽԺÿ�������Ϻ�������֢������y�뵱��Ŀ�������![]() ��
��![]() ȡ�������������¹�ϵ
ȡ�������������¹�ϵ![]() �ҵ�t��300ʱ��y��500��������ijһҽԺ���δ��ಡ֢��������200�˵ĸ��ʣ�
�ҵ�t��300ʱ��y��500��������ijһҽԺ���δ��ಡ֢��������200�˵ĸ��ʣ�
��2�����ڣ�1���У���t��300ʱ��y��t�Ĺ�ϵ��ϵ�����Ϊ![]() ������ȡ����10���������ݣ�ti��yi����i=1��2��3������10������֪
������ȡ����10���������ݣ�ti��yi����i=1��2��3������10������֪![]()
![]() ���ÿ����Ի��Ļع鷽������������ߵı���ʽ�����������Իع鷽��
���ÿ����Ի��Ļع鷽������������ߵı���ʽ�����������Իع鷽��![]() �У�
�� 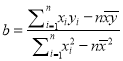 ��
�� ![]() ����
����
���𰸡���1��![]() ����2��
����2��![]()
�������������������1��ҪʹijһҽԺ���δ��ಡ֢��������![]() �ˣ���
�ˣ���![]() ,��������������������
,��������������������![]() �죬���ùŵ�����ʹ�ʽ�ɵý������2����
�죬���ùŵ�����ʹ�ʽ�ɵý������2����![]() ,����ƽ��ֵ��ʽ���
,����ƽ��ֵ��ʽ���![]() ��ƽ��ֵ���ɵ��������ĵ�����꣬�����������������ݣ����ù�ʽ
��ƽ��ֵ���ɵ��������ĵ�����꣬�����������������ݣ����ù�ʽ �����
�����![]() ������������ĵ����������
������������ĵ����������![]() ���Ӷ��ɵ����Իع鷽��.
���Ӷ��ɵ����Իع鷽��.
�����������1��ҪʹijһҽԺ���δ��ಡ֢��������200�ˣ���t>150,��������������������50�죬���Ը���Ϊ![]() .
.
(2)�� ![]() ����
����![]()
![]() ��
��![]() ��
��![]()
![]()
![]()
![]() ��
��![]()
![]() �� ����
�� ����![]()
 ��
��![]() ������������ߵı���ʽΪ
������������ߵı���ʽΪ![]()

 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д� â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�

