题目内容
设O中△ABC的外心,
=
,
=
,且|
|=|
|,则
可用
,
表示为( )
| AB |
| a |
| AC |
| b |
| a |
| b |
| AO |
| a |
| b |
分析:利用已知条件表示出向量
的模,以及
的单位向量,利用|
|=|
|,然后求出
,得到选项.
| AO |
| AO |
| a |
| b |
| AO |
解答:解:三角形的外心是指三边中垂线的交点,延长AO到D,D在BC上AD是BC的中垂线,
AD⊥BC,BD=
BC过点O作OE⊥AB,E在AB上OE是AB的中垂线,AE=
AB
则cos∠BAD=
=
,AO=
,AB=|
|,AE=
|
|,AD=
|
+
|
∴|
|=
=
,设沿
方向的单位向量为
,
则
=
∴
=|
|*
=
•
∵
2=|
|2=|
|2=
2
∴
=
(
+
)=
(
+
).
故选A.
AD⊥BC,BD=
| 1 |
| 2 |
| 1 |
| 2 |
则cos∠BAD=
| AE |
| AO |
| AD |
| AB |
| AB•AE |
| AD |
| a |
| 1 |
| 2 |
| a |
| 1 |
| 2 |
| a |
| b |
∴|
| AO |
|
| ||||||
|
|
| ||||
|
|
| AO |
| e |
则
| e |
| ||||
|
|
∴
| AO |
| AO |
| e |
|
| ||||
|
|
| ||||
|
|
∵
| a |
| a |
| b |
| b |
∴
| AO |
| ||||||||
|
| a |
| b |
| ||||||
2(
|
| a |
| b |
故选A.
点评:本题考查向量在几何中的应用,向量的表示方法,三角形的外心的应用,考查计算能力转化思想.

练习册系列答案
相关题目
设O为△ABC的外心,且3
+4
+5
=
,则△ABC中的内角C值为( )
| OA |
| OB |
| OC |
| 0 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 =
= ,
, =
= ,且|
,且| |=|
|=|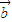 |,则
|,则 可用
可用 ,
,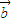 表示为( )
表示为( ) (
( +
+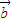 )
) +
+ )
) (
( +
+ )
) (
( +
+ )
) B.
B.