题目内容
设{an}(n∈N*)是等差数列,Sn是其前n项的和,已知S7=7,S15=75,Tn是数列{
思路解析:本题考查等差数列的定义、前n项和公式以及具体应用.由题意不难得知,可先求出首项和公差,从而表示出Sn,进而表示出![]() ,通过判断它是等差数列,从而求得Tn.
,通过判断它是等差数列,从而求得Tn.
解:设等差数列{an}的公差是d,
则由题意有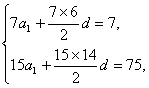 由此解得a1=-2,d=1,∴
由此解得a1=-2,d=1,∴![]() ,
,
![]()
![]() ,
,![]() .∴数列{
.∴数列{![]() }是以-2为首项、
}是以-2为首项、![]() 为公差的等差数列,
为公差的等差数列,
Tn=![]() n2-
n2-![]() n.
n.

练习册系列答案
相关题目
题目内容
设{an}(n∈N*)是等差数列,Sn是其前n项的和,已知S7=7,S15=75,Tn是数列{
思路解析:本题考查等差数列的定义、前n项和公式以及具体应用.由题意不难得知,可先求出首项和公差,从而表示出Sn,进而表示出![]() ,通过判断它是等差数列,从而求得Tn.
,通过判断它是等差数列,从而求得Tn.
解:设等差数列{an}的公差是d,
则由题意有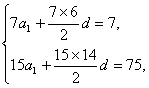 由此解得a1=-2,d=1,∴
由此解得a1=-2,d=1,∴![]() ,
,
![]()
![]() ,
,![]() .∴数列{
.∴数列{![]() }是以-2为首项、
}是以-2为首项、![]() 为公差的等差数列,
为公差的等差数列,
Tn=![]() n2-
n2-![]() n.
n.
