题目内容
如图,已知椭圆长轴端点A、B,弦EF与AB交于点D,O为中心,且|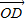 |=1,
|=1,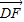 =2
=2 ,∠FDO=
,∠FDO= ,试建立适当的坐标系解决以下问题:
,试建立适当的坐标系解决以下问题:(1)求椭圆的长轴长的取值范围;
(2)若D为椭圆的焦点,求椭圆的方程.

【答案】分析:(1)建立如图平面直角坐标系,则D(-1,0)弦EF所在的直线方程为y=x+1,设椭圆方程 ,将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用长轴的表示的函数式即可求得范围,从而解决问题.
,将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用长轴的表示的函数式即可求得范围,从而解决问题.
(2)利用D为椭圆的焦点,则c=1,b2=a2-1结合(1)知:∴a2=9-a2 从而求出a,b的值,最后写出椭圆方程即可.
解答:解:(1)如图,建立平面直角坐标系,则D(-1,0)弦EF所在的直线方程为y=x+1
设椭圆方程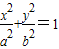 设E(x1,y1),F(x2,y2),
设E(x1,y1),F(x2,y2),
由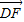 =2
=2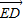 ,知:y1+y2=-y1,且y1y2=-2y12 联立方程组
,知:y1+y2=-y1,且y1y2=-2y12 联立方程组 ,
,
消去x得:(a2+b2)y2-2b2y+b2-a2b2=0
由题意知:a>1,∴△=4b4=4(a2+b2)(b2-a2b2)>0
由韦达定理知:y1+y2=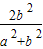 =-y1,y1y2=
=-y1,y1y2=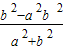 =-2y12,
=-2y12,
消去y1得化简整理得:b2= ∵0<b2<a2,∴0<
∵0<b2<a2,∴0<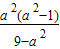 <a2解得:
<a2解得:
1<a2<5
∴2<2a<2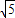 即:椭圆的长轴长的取值范围为(2,2
即:椭圆的长轴长的取值范围为(2,2 ).
).
(2)若D为椭圆的焦点,则c=1,b2=a2-1
由(1)知:b2=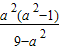 =a2-1,
=a2-1,
∴a2=9-a2∴a2= ,b2=
,b2= ∴椭圆方程为:
∴椭圆方程为: .
.
点评:本题以椭圆为载体,考查直线与椭圆的位置关系,关键是直线与椭圆方程的联立,利用韦达定理可解.解题时要认真审题,注意挖掘题设中的隐含条件,注意合理地进行等价转化.
 ,将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用长轴的表示的函数式即可求得范围,从而解决问题.
,将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用长轴的表示的函数式即可求得范围,从而解决问题.(2)利用D为椭圆的焦点,则c=1,b2=a2-1结合(1)知:∴a2=9-a2 从而求出a,b的值,最后写出椭圆方程即可.
解答:解:(1)如图,建立平面直角坐标系,则D(-1,0)弦EF所在的直线方程为y=x+1
设椭圆方程
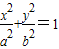 设E(x1,y1),F(x2,y2),
设E(x1,y1),F(x2,y2),由
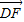 =2
=2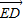 ,知:y1+y2=-y1,且y1y2=-2y12 联立方程组
,知:y1+y2=-y1,且y1y2=-2y12 联立方程组 ,
,消去x得:(a2+b2)y2-2b2y+b2-a2b2=0
由题意知:a>1,∴△=4b4=4(a2+b2)(b2-a2b2)>0
由韦达定理知:y1+y2=
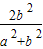 =-y1,y1y2=
=-y1,y1y2=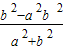 =-2y12,
=-2y12,消去y1得化简整理得:b2=
 ∵0<b2<a2,∴0<
∵0<b2<a2,∴0<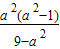 <a2解得:
<a2解得:1<a2<5
∴2<2a<2
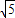 即:椭圆的长轴长的取值范围为(2,2
即:椭圆的长轴长的取值范围为(2,2 ).
).(2)若D为椭圆的焦点,则c=1,b2=a2-1
由(1)知:b2=
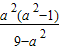 =a2-1,
=a2-1,∴a2=9-a2∴a2=
 ,b2=
,b2= ∴椭圆方程为:
∴椭圆方程为: .
.点评:本题以椭圆为载体,考查直线与椭圆的位置关系,关键是直线与椭圆方程的联立,利用韦达定理可解.解题时要认真审题,注意挖掘题设中的隐含条件,注意合理地进行等价转化.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
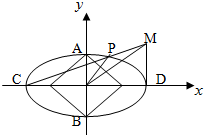 如图,已知椭圆
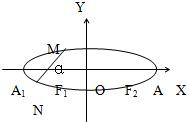
如图,已知椭圆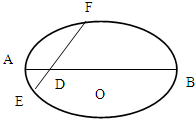 如图,已知椭圆长轴端点A、B,弦EF与AB交于点D,O为中心,且|
如图,已知椭圆长轴端点A、B,弦EF与AB交于点D,O为中心,且| ,过椭圆焦点F1作一直线,交椭圆于两点M,N,设∠F2F1M=α(0≤α<π)当α取什么值时,|MN|等于椭圆短轴的长?
,过椭圆焦点F1作一直线,交椭圆于两点M,N,设∠F2F1M=α(0≤α<π)当α取什么值时,|MN|等于椭圆短轴的长?