题目内容
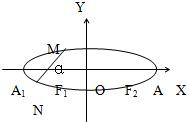
如图,已知椭圆长轴|A1A2|=6,焦距|F1F2|= ,过椭圆焦点F1作一直线,交椭圆于两点M,N,设∠F2F1M=α(0≤α<π)当α取什么值时,|MN|等于椭圆短轴的长?
,过椭圆焦点F1作一直线,交椭圆于两点M,N,设∠F2F1M=α(0≤α<π)当α取什么值时,|MN|等于椭圆短轴的长?
【答案】分析:解一:以椭圆焦点F1为极点,以F1为起点并过F2的射线为极轴建立极坐标系,由已知条件可知椭圆的极坐标方程为 ∴
∴ ,
,
 据此能够求出α的取值.
据此能够求出α的取值.
解二:以椭圆的中心为原点,F1F2所在直线为x轴建立直角坐标系(如图)由已知条件知,椭圆的方程为 MN所在直线方程为
MN所在直线方程为 (其中k=tanα),联立方程组后由题设条件能够推导出α的取值.
(其中k=tanα),联立方程组后由题设条件能够推导出α的取值.
解三:建立坐标系得椭圆方程为 MN所在直线的参数方程为
MN所在直线的参数方程为 ,y=tsinα(t是参数)代入椭圆方程得
,y=tsinα(t是参数)代入椭圆方程得 设t1,t2是方程两根,则由韦达定理结合题设条件能够推陈出新导出α的取值.
设t1,t2是方程两根,则由韦达定理结合题设条件能够推陈出新导出α的取值.
解四:设|F1M|=x,则|F2M|=6-x|F1F2|= ,∠F2F1M=α,在△MF1F2中由余弦定理结合题设条件能够推陈出新导出α的取值.
,∠F2F1M=α,在△MF1F2中由余弦定理结合题设条件能够推陈出新导出α的取值.
解答:解:法一:以椭圆焦点F1为极点,
以F1为起点并过F2的射线为极轴建立极坐标系
由已知条件可知椭圆长半轴a=3,
半焦距c= ,短半轴b=1,
,短半轴b=1,
离心率e= ,中心到准线距离=
,中心到准线距离= ,
,
焦点到准线距离p= .
.
椭圆的极坐标方程为
∴ ,
,
 .
.
解得 .∴
.∴ 或
或 .
.
以上解方程过程中的每一步都是可逆的,
所以当 或
或 时,|MN|等于短轴的长.
时,|MN|等于短轴的长.
法二:以椭圆的中心为原点,
F1F2所在直线为x轴建立直角坐标系(如图)由已知条件知,椭圆的方程为 .
.
MN所在直线方程为 (其中k=tanα)
(其中k=tanα)
解方程组 .
.
消去y得 .
. =
=
= ,解得
,解得 .∴
.∴ 或
或 .
.
所以当 或
或 时,|MN|等于短轴的长
时,|MN|等于短轴的长
法三:建立坐标系得椭圆方程为 .
.
MN所在直线的参数方程为 (t是参数)
(t是参数)
代入椭圆方程得 .
.
设t1,t2是方程两根,则由韦达定理,
 .
.
 .=
.= ,
,
解得 .∴
.∴ 或
或 .
.
所以当 或
或 时,|MN|等于短轴的长
时,|MN|等于短轴的长
法四:设|F1M|=x,则|F2M|=6-x
|F1F2|= ,∠F2F1M=α
,∠F2F1M=α
在△MF1F2中由余弦定理得
 ,
,


同理,设|F1N|=y,则|F2N|=6-y在△F1F2N中,由余弦定理得
 .
.
 ,
,
 =2,解得
=2,解得 .
.
∴ 或
或 .
.
所以当 或
或 时,|MN|等于短轴的长.
时,|MN|等于短轴的长.
点评:一题多解能够有首席地提高我们的解题能力,不时练习时要多尝试一题多解.
 ∴
∴ ,
, 据此能够求出α的取值.
据此能够求出α的取值.解二:以椭圆的中心为原点,F1F2所在直线为x轴建立直角坐标系(如图)由已知条件知,椭圆的方程为
 MN所在直线方程为
MN所在直线方程为 (其中k=tanα),联立方程组后由题设条件能够推导出α的取值.
(其中k=tanα),联立方程组后由题设条件能够推导出α的取值.解三:建立坐标系得椭圆方程为
 MN所在直线的参数方程为
MN所在直线的参数方程为 ,y=tsinα(t是参数)代入椭圆方程得
,y=tsinα(t是参数)代入椭圆方程得 设t1,t2是方程两根,则由韦达定理结合题设条件能够推陈出新导出α的取值.
设t1,t2是方程两根,则由韦达定理结合题设条件能够推陈出新导出α的取值.解四:设|F1M|=x,则|F2M|=6-x|F1F2|=
 ,∠F2F1M=α,在△MF1F2中由余弦定理结合题设条件能够推陈出新导出α的取值.
,∠F2F1M=α,在△MF1F2中由余弦定理结合题设条件能够推陈出新导出α的取值.解答:解:法一:以椭圆焦点F1为极点,
以F1为起点并过F2的射线为极轴建立极坐标系
由已知条件可知椭圆长半轴a=3,
半焦距c=
 ,短半轴b=1,
,短半轴b=1,离心率e=
 ,中心到准线距离=
,中心到准线距离= ,
,焦点到准线距离p=
 .
.椭圆的极坐标方程为

∴
 ,
, .
.解得
 .∴
.∴ 或
或 .
.以上解方程过程中的每一步都是可逆的,
所以当
 或
或 时,|MN|等于短轴的长.
时,|MN|等于短轴的长.法二:以椭圆的中心为原点,
F1F2所在直线为x轴建立直角坐标系(如图)由已知条件知,椭圆的方程为
 .
.MN所在直线方程为
 (其中k=tanα)
(其中k=tanα)解方程组
 .
.消去y得
 .
. =
=
=
 ,解得
,解得 .∴
.∴ 或
或 .
.所以当
 或
或 时,|MN|等于短轴的长
时,|MN|等于短轴的长法三:建立坐标系得椭圆方程为
 .
.MN所在直线的参数方程为
 (t是参数)
(t是参数)代入椭圆方程得
 .
.设t1,t2是方程两根,则由韦达定理,
 .
. .=
.= ,
,解得
 .∴
.∴ 或
或 .
.所以当
 或
或 时,|MN|等于短轴的长
时,|MN|等于短轴的长法四:设|F1M|=x,则|F2M|=6-x
|F1F2|=
 ,∠F2F1M=α
,∠F2F1M=α在△MF1F2中由余弦定理得
 ,
,

同理,设|F1N|=y,则|F2N|=6-y在△F1F2N中,由余弦定理得
 .
. ,
, =2,解得
=2,解得 .
.∴
 或
或 .
.所以当
 或
或 时,|MN|等于短轴的长.
时,|MN|等于短轴的长.点评:一题多解能够有首席地提高我们的解题能力,不时练习时要多尝试一题多解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
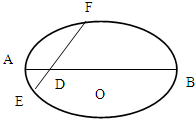 如图,已知椭圆长轴端点A、B,弦EF与AB交于点D,O为中心,且|
如图,已知椭圆长轴端点A、B,弦EF与AB交于点D,O为中心,且| 是长轴为
是长轴为 的椭圆上三点,点
的椭圆上三点,点 是长轴的一个顶点,
是长轴的一个顶点, 过椭圆中心
过椭圆中心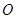 ,且
,且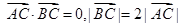 .
.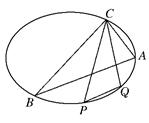
 使直线
使直线 与
与 轴围成底边在
轴围成底边在 使
使 ?请给出证明.
?请给出证明.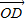 |=1,
|=1,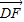 =2
=2 ,∠FDO=
,∠FDO= ,试建立适当的坐标系解决以下问题:
,试建立适当的坐标系解决以下问题: