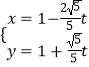题目内容
【题目】已知椭圆C： 
（a＞b＞0）左、右焦点分别为F1 ， F2 ， A（2，0）是椭圆的右顶点，过F2且垂直于x轴的直线交椭圆于P，Q两点，且|PQ|=3；
（1）求椭圆的方程；
（2）若直线l与椭圆交于两点M，N（M，N不同于点A），若 
=0， 
= 
；
①求证：直线l过定点；并求出定点坐标；
②求直线AT的斜率的取值范围．
【答案】
（1）
解：由题意可知：a=2，
令x=c，代入椭圆方程，解得：y= 
，则丨PQ丨= 
=3，
则b= 
，
∴椭圆的标准方程为： 
（2）
解：①当直线MN斜率不存在时，设lMN：x=m，
则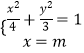 
，解得：y= 
，则丨MN丨=2 ，
设直线MN与x轴交于点B，丨丨MB=丨AM丨即 =2﹣m，
∴m= 
或m=2（舍），
∴直线lMN过定点（ ，0）；
当直线MN斜率存在时，设直线MN斜率为k，
设M（x1，y1），N（x2，y2），则直线MN：y=kx+b，
与椭圆方程 ，联立，消取y整理得（4k2+3）x2+8kbx+4k2﹣12=0，
∴x1+x2=﹣ 
，x1x2= 
，
△＞0，k∈R，
=0，（x1﹣2，y1）（x2﹣2，y2）=0，
即x1x2﹣2（x1+x2）+4+y1y2=0，
y1y2=（kx1+b）（kx2+b）=k2x1x2+kb（x1+x2）+b2= 
，
∴7b2+4k2+16kb=0，则b=﹣ k，或b=﹣2k，
∴lMN：y=k（x﹣ ）或y=k（x﹣2），
∴直线lMN过定点（ ，0）或（2，0）；
综合知，直线过定点（ ，0）；
②T为MN中点，T（ 
， ），则T（﹣
， 
），
∴kAT=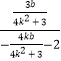 
= 
，
由b=﹣ 
，则kAT= 
，
当k=0时，kAT=0，
当k≠0时，k∈R，kAT= = 
，
由8k+ 
≥2 
=2 
，
或8k+ ≤﹣2 =﹣2 ，
∴kAT∈[﹣ 
， ]，
直线AT的斜率的取值范围为[﹣ ， ]
【解析】（1）由a=2，则椭圆的通径丨PQ丨= ，代入即可求得b的值，即可取得椭圆的方程；（2）当直线MN斜率不存在时，将x=m代入椭圆方程，则 =2﹣m，即可求得m的值，即可求得直线恒过定点；当斜率存在，设直线方程y=kx+b，代入椭圆方程，由韦达定理，向量的坐标运算，即可求得b=﹣ k，或b=﹣2k，即可求得直线方程，则直线过定点（ ，0）；（3）利用中点坐标公式求得T坐标，利用直线的斜率公式，kAT= = ，分类当k=0，kAT=0，当k≠0时，利用基本不等式的性质，即可求得直线AT的斜率的取值范围．
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识，掌握椭圆标准方程焦点在x轴：
，焦点在y轴：
．
