题目内容
函数![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() .
.
(1)求实数![]() 的值,并确定函数
的值,并确定函数![]() 的解析式;
的解析式;
(2)用定义证明![]() 在
在![]() 的单调性,并判断
的单调性,并判断![]() 在
在![]() 的单调性情况;
的单调性情况;
(3)根据第(2)推断总结函数![]() 在
在![]() 上单调性情况,并由此你能否得到函数
上单调性情况,并由此你能否得到函数![]() 在
在![]() 上的单调性(写出单调区间及单调性)
上的单调性(写出单调区间及单调性)
解:(1)![]()
![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]()
![]()
 解得
解得![]()
![]()
![]() …………4分
…………4分
(2)设 ![]()
![]() …………6分
…………6分
①![]() 时,
时,![]() ,
,![]()
![]()
![]()
![]()
![]() 上单调递减。 …………8分
上单调递减。 …………8分
②![]() 时,
时,![]() ,
,![]()
![]()
![]()
![]()
![]() 上单调递增。 …………10分
上单调递增。 …………10分
判断![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增。 …………11分
上单调递增。 …………11分
(3)![]() (
(![]() )在
)在![]() 上单调递减,在
上单调递减,在![]() 上单调递增。 …13分
上单调递增。 …13分
根据奇偶性![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减。 ……14分
上单调递减。 ……14分

练习册系列答案
相关题目
 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,
, 的解析式;
的解析式; .
. 是定义在R上的奇函数,且
是定义在R上的奇函数,且 ,在[0,2]上
,在[0,2]上 ,则
,则 ;[来源:Z§xx§k.Com]
;[来源:Z§xx§k.Com] 且
且 ;
; 在[-8,8]内恰有四个不同的根
在[-8,8]内恰有四个不同的根 ,则
,则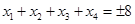 ;
;