题目内容
【题目】已知函数![]() 有两个极值点
有两个极值点![]() ,
, ![]() (
(![]() ).
).
(1)求实数![]() 的取值范围;
的取值范围;
(2)设![]() ,若函数
,若函数![]() 的两个极值点恰为函数
的两个极值点恰为函数![]() 的两个零点,当
的两个零点,当![]() 时,求
时,求![]() 的最小值.
的最小值.
【答案】(1)![]() .(2)
.(2)![]() .
.
【解析】试题分析:(I)求出函数f(x)的导数,可得方程x2-ax+1=0有两个不相等的正根,即可求出a的范围;(II)对函数g(x)求导数,利用极值的定义得出g'(x)=0时存在两正根x1,x2;再利用判别式以及根与系数的关系,结合零点的定义,构造函数,利用导数即可求出函数y的最小值
解析:
(1)![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
令![]() ,即
,即![]() ,要使
,要使![]() 在
在![]() 上有两个极值点,
上有两个极值点,
则方程![]() 有两个不相等的正根,
有两个不相等的正根,
则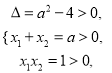 解得
解得![]() ,
,
即![]() .
.
(2)![]() ,
,
由于![]() ,
, ![]() 为
为![]() 的两个零点,
的两个零点,
即![]() ,
, ![]() ,
,
两式相减得: ![]() .
.
∴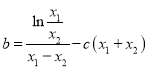 ,
,
又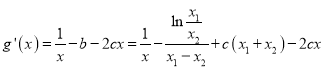 ,
,
∴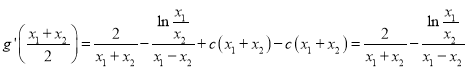 ,
,
故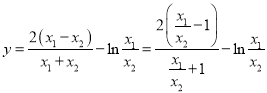 ,
,
设![]() ,∵
,∵![]() ,
, ![]() 为
为![]() 的两根,
的两根,
∴![]() 故
故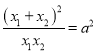 ,
,
∴![]() ,又
,又![]() ,
,
即![]() ,
,
解得![]() 或
或![]() ,
,
因此![]() ,
,
此时![]() ,
,
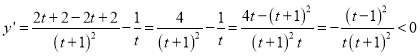 ,
,
即函数![]() 在
在![]() 单调递减,
单调递减,
∴当![]() 时,
时, ![]() 取得最小值,
取得最小值,
∴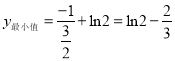 .
.
即所求最小值为![]() .
.

练习册系列答案
相关题目
【题目】某厂拟用集装箱托运甲、乙两种货物,集装箱的体积、重量、可获利润和托运能力等限制数据列在表中,如何设计甲、乙两种货物应各托运的箱数可以获得最大利润,最大利润是多少?
货物 | 体积 | 重量 | 利润 |
甲 | 5 | 2 | 20 |
乙 | 4 | 5 | 10 |
托运限制 | 24 | 13 |
【题目】某仪器经过检验合格才能出厂,初检合格率为![]() :若初检不合格,则需要进行调试,经调试后再次对其进行检验;若仍不合格,作为废品处理,再检合格率为
:若初检不合格,则需要进行调试,经调试后再次对其进行检验;若仍不合格,作为废品处理,再检合格率为![]() .每台仪器各项费用如表:
.每台仪器各项费用如表:
项目 | 生产成本 | 检验费/次 | 调试费 | 出厂价 |
金额(元) | 1000 | 100 | 200 | 3000 |
(Ⅰ)求每台仪器能出厂的概率;
(Ⅱ)求生产一台仪器所获得的利润为1600元的概率(注:利润![]() 出厂价
出厂价![]() 生产成本
生产成本![]() 检验费
检验费![]() 调试费);
调试费);
(Ⅲ)假设每台仪器是否合格相互独立,记![]() 为生产两台仪器所获得的利润,求
为生产两台仪器所获得的利润,求![]() 的分布列和数学期望.
的分布列和数学期望.