题目内容
如图,长方体ABCD—A1B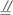
证明:分别在AB、CD上截取AE=A1E1,DF=D
∵长方体AC1的各个面是矩形,∴A1E1∥AE,D
故四边形AEE
∴EE1![]() AA1,FF1
AA1,FF1![]() DD1.
DD1.
∵AA1![]() DD1,
DD1,
∴EE1![]() FF1.
FF1.
∴四边形EFF1E1是平行四边形.
∴E
∵EF![]() 平面AC,E
平面AC,E![]() 平面AC,∴E
平面AC,∴E

练习册系列答案
相关题目
题目内容
如图,长方体ABCD—A1B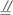
证明:分别在AB、CD上截取AE=A1E1,DF=D
∵长方体AC1的各个面是矩形,∴A1E1∥AE,D
故四边形AEE
∴EE1![]() AA1,FF1
AA1,FF1![]() DD1.
DD1.
∵AA1![]() DD1,
DD1,
∴EE1![]() FF1.
FF1.
∴四边形EFF1E1是平行四边形.
∴E
∵EF![]() 平面AC,E
平面AC,E![]() 平面AC,∴E
平面AC,∴E
