题目内容
双曲线kx2-y2=1的一条渐近线与直线2x+y+1=0垂直，则此双曲线的离心率是
- A.
- B.
- C.
- D.
A
分析：分析：已知双曲线kx2-y2=1的一条渐近线与直线2x+y+1=0垂直，可求出渐近线的斜率，由此求出k的值，得到双曲线的方程，再求离心率
解答：设双曲线kx2-y2=1为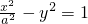
，它的一条渐近线方程为 
直线2x+y+1=0的斜率为-2
∵直线与直线2x+y+1=0垂直
∴
即a=2
∴
故选A．
点评：本题考查直线与圆锥曲线的关系，解题的关键是理解一条渐近线与直线2x+y+1=0垂直，由此关系求k，熟练掌握双曲线的性质是求解本题的知识保证．
分析：分析：已知双曲线kx2-y2=1的一条渐近线与直线2x+y+1=0垂直，可求出渐近线的斜率，由此求出k的值，得到双曲线的方程，再求离心率
解答：设双曲线kx2-y2=1为
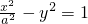，它的一条渐近线方程为 直线2x+y+1=0的斜率为-2
∵直线
与直线2x+y+1=0垂直∴
即a=2∴
故选A．
点评：本题考查直线与圆锥曲线的关系，解题的关键是理解一条渐近线与直线2x+y+1=0垂直，由此关系求k，熟练掌握双曲线的性质是求解本题的知识保证．
练习册系列答案
相关题目
双曲线kx2-y2=1的一个焦点是(
，0)，那么它的实轴长是（ ）
| 2 |
| A、1 | ||
| B、2 | ||
C、
| ||
D、2
|