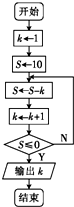
题目内容
5．若tanθ=1，则sin2θ的值为（ ）| A． | $\frac{\sqrt{2}}{2}$ | B． | 1 | C． | $\frac{1}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |
分析 原式利用二倍角的正弦函数公式化简，分母看做“1”，利用同角三角函数间的基本关系变形，将tanθ的值代入计算即可求出值．
解答 解：∵tanθ=1，
∴sin2θ=$\frac{2sinθcosθ}{si{n}^{2}θ+co{s}^{2}θ}$=$\frac{2tanθ}{ta{n}^{2}θ+1}$=1．
故选：B．
点评 此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
春雨教育同步作文系列答案
相关题目
20．设△ABC的内角A，B，C所对的边长分别为a，b，c，且atanB=$\frac{20}{3}$，bsinA=4，则a等于（ ）
| A． | 3 | B． | $\frac{8}{3}$ | C． | 4 | D． | 5 |
10．在数列{an}中，若存在一个确定的正整数T，对任意n∈N*满足an+T=an，则称{an}是周期数列，T叫做它的周期．已知数列{xn}满足x1=1，x2=a（a≤1），xn+2=|xn+1-xn|，若数列{xn}的周期为3，则{xn}的前2014项的和为（ ）
| A． | 1344 | B． | 1343 | C． | 1224 | D． | 1223 |
17．
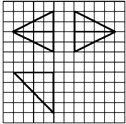如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为（ ）
如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为（ ）| A． | 2$\sqrt{5}$ | B． | 2$\sqrt{6}$ | C． | 4$\sqrt{2}$ | D． | 4$\sqrt{3}$ |
14．若|$\overrightarrow{e}$|=1，且$\overrightarrow{a}⊥\overrightarrow{e}$，|$\overrightarrow{a}$|=2，则|4$\overrightarrow{a}-\overrightarrow{e}$|=（ ）
| A． | $\sqrt{37}$ | B． | $\sqrt{65}$ | C． | 8 | D． | $\sqrt{13}$ |