题目内容
如图所示,在我国西部某地区,有四个村庄A、B、C、D恰好坐落在边长为2 km的正方形的顶点上,为改善农业饮水质量,政府决定在水质较好的正方形中心O处新建一个水厂,向四个村庄供水.为节约成本,降低工程造价,请你设计一种最佳方案,使铺设的输水管道最短.
由正方形的对称性,设应铺设的与AB垂直的中心输水管道长为2x km,设输水管道的总长为y km,则依题意得y=2x+4
即(y-2x)2=16(x2-2x+2),化简,得12x2+(4y-32)x+32-y2=0.①
∵x∈R+,∴Δ=(4y-32)2-4×12(32-y2)≥0,即y2-4y-8≥0.
∵y>0,
∴y≥2+2
.将y的最小值2+2
代入①,方程①有等根,
此时x=-
∈R+.
∴中心输水管道长为(2-
) km时,输水管道总长最短.
练习册系列答案
相关题目
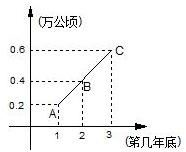全世界每年都有大量土地被沙漠吞没，保护土地资源，已成为一项十分紧迫的任务．据统计，在我国西部地区，1998年共有沙漠面积100万公顷，1999年至2002年三年的沙漠面积变化情况如图所示（图中横轴数字表示时间，1，2，3分别表示第1，2，3年年底；纵轴数字表示相应时间对应的沙漠面积比原有面积的增加数；A，B，C三点在一条直线上）．经过专家考察预测，该地区的沙漠面积若干年内将继续按此规律扩大．若以1999年为第1年进行计算，
全世界每年都有大量土地被沙漠吞没，保护土地资源，已成为一项十分紧迫的任务．据统计，在我国西部地区，1998年共有沙漠面积100万公顷，1999年至2002年三年的沙漠面积变化情况如图所示（图中横轴数字表示时间，1，2，3分别表示第1，2，3年年底；纵轴数字表示相应时间对应的沙漠面积比原有面积的增加数；A，B，C三点在一条直线上）．经过专家考察预测，该地区的沙漠面积若干年内将继续按此规律扩大．若以1999年为第1年进行计算，