题目内容
记数列{an}所有项的和为S（1），第二项及以后各项的和为S（2），第三项及以后各项的和为S（3），…，第n项及以后各项的和为S（n），若S（1）=2，S（2）=1，S（3）=
，…，S（n）=
…，则an=（ ）A．
B．
C．
D．
【答案】分析：由已知中S（n）=
表示自n项往后的所有项的和，可得S（n-1）=
=2×
表示自n-1项往后的所有项的和，两式相减，即可得到S（n-1）-S（n）=an-1，进而得到答案．
解答：解：∵S（n）=
，则S（n）表示自n项往后的所有项的和．
∴S（n-1）=
=2×
，则表示自n-1项往后的所有项的和．
两式相减的结果，是数列{an}的第n-1项，
即：S（n-1）-S（n）=an-1=2×
-
=
，
∴an=
故选C
点评：本题考查的知识点是归纳推理，其中正确理解S（n-1）-S（n）=an-1，是解答本题的关键，本题是一个新定义，易犯经验主义错误，而错认为S（n-1）-S（n）=-an，而得到错解．
表示自n项往后的所有项的和，可得S（n-1）==2×表示自n-1项往后的所有项的和，两式相减，即可得到S（n-1）-S（n）=an-1，进而得到答案．解答：解：∵S（n）=
，则S（n）表示自n项往后的所有项的和．∴S（n-1）=
=2×，则表示自n-1项往后的所有项的和．两式相减的结果，是数列{an}的第n-1项，
即：S（n-1）-S（n）=an-1=2×
-=，∴an=
故选C
点评：本题考查的知识点是归纳推理，其中正确理解S（n-1）-S（n）=an-1，是解答本题的关键，本题是一个新定义，易犯经验主义错误，而错认为S（n-1）-S（n）=-an，而得到错解．
练习册系列答案
相关题目
,…,S(n)=
,…,则an等于
B.
C.
D.
，…，S（n）=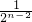
…，则an=
