题目内容
椭圆C的中心为坐标原点O,焦点在y轴上,离心率e = ![]() ,椭圆上的点到焦点的最短距离为1-
,椭圆上的点到焦点的最短距离为1-![]() , 直线l与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且
, 直线l与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且![]() .
.
(1)求椭圆方程;
(2)若![]() ,求m的取值范围.
,求m的取值范围.
(1)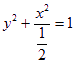 (2)(-1,-
(2)(-1,-![]() )∪(
)∪(![]() ,1)∪{0}
,1)∪{0}
解析:
(1)设C:+=1(a>b>0),设c>0,c2=a2-b2,由条件知a-c=![]() ,=
,=![]() ,
,
∴a=1,b=c=![]() ,
,
故C的方程为: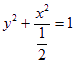 5′
5′
(2)由=λ,![]()
∴λ+1=4,λ=3 或O点与P点重合= 7′
当O点与P点重合=时,m=0
当λ=3时,直线l与y轴相交,则斜率存在。
设l与椭圆C交点为A(x1,y1),B(x2,y2)
得(k2+2)x2+2kmx+(m2-1)=0
Δ=(2km)2-4(k2+2)(m2-1)=4(k2-2m2+2)>0 (*)
x1+x2=, x1x2= 11′
∵=3 ∴-x1=3x2 ∴
消去x2,得3(x1+x2)2+4x1x2=0,∴3()2+4=0
整理得4k2m2+2m2-k2-2=0 13′
m2=![]() 时,上式不成立;m2≠
时,上式不成立;m2≠![]() 时,k2=,
时,k2=,
因λ=3 ∴k≠0 ∴k2=>0,∴-1<m<-![]() 或
或 ![]() <m<1
<m<1
容易验证k2>2m2-2成立,所以(*)成立
即所求m的取值范围为(-1,-![]() )∪(
)∪(![]() ,1)∪{0} 16′
,1)∪{0} 16′

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目