题目内容
已知点A(1,,0),B(0,,1),C(2sinθ,cosθ).(Ⅰ)若|
| AC |
| BC |
(Ⅱ)设O为坐标原点,点C在第一象限,求函数y=(
| OA |
| OB |
| OC |
分析:(I)表示出
和
向量,然后根据 |
|=|
|,可求得tanθ的值.
(Ⅱ)首先表示出向量
=(1,0),
=(0,1),
=(2sinθ,cosθ),进而求出函数的解析式并化简y=2
sin(θ+
)即可求出单调区间和值域.
| AC |
| BC |
| AC |
| BC |
(Ⅱ)首先表示出向量
| OA |
| OB |
| OC |
| 2 |
| π |
| 4 |
解答:解:(Ⅰ)∵A(1,0),B(0,1),C(2sinθ,cosθ)
∵
=(2sinθ-1,cosθ),
=(2sinθ,cosθ-1)
∵|
|=|
|
∴
=
化简得2sinθ=cosθ.
∵cosθ≠0(若cosθ=0,则sinθ=±1,上式不成立),
∴tanθ=
…(6分)
(Ⅱ)∵
=(1,0),
=(0,1),
=(2sinθ,cosθ),
∴y=2sinθ+2cosθ
=2
sin(θ+
)
∴求函数的单调递增区间为(2kπ,2kπ+
],(k∈z)
值域是(2,2
](14分)
∵
| AC |
| BC |
∵|
| AC |
| BC |
∴
| (2sinθ-1)2+cos2θ |
| (2sinθ)2+(cosθ-1)2 |
化简得2sinθ=cosθ.
∵cosθ≠0(若cosθ=0,则sinθ=±1,上式不成立),
∴tanθ=
| 1 |
| 2 |
(Ⅱ)∵
| OA |
| OB |
| OC |
∴y=2sinθ+2cosθ
=2
| 2 |
| π |
| 4 |
∴求函数的单调递增区间为(2kπ,2kπ+
| π |
| 4 |
值域是(2,2
| 2 |
点评:本题考查平面向量的数量积,向量的模,同角三角函数的基本关系式,是中档题.

练习册系列答案
相关题目
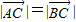 ,求tanθ的值;
,求tanθ的值;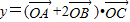 的单调递增区间与值域.
的单调递增区间与值域.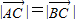 ,求tanθ的值;
,求tanθ的值;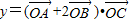 的单调递增区间与值域.
的单调递增区间与值域.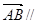 a,且
a,且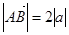 ,则B点的坐标为
,则B点的坐标为