题目内容
设向量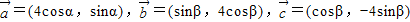
(1)若
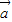 与
与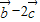 垂直,求tan(α+β)的值;
垂直,求tan(α+β)的值;(2)求
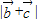 的最大值;
的最大值;(3)若tanαtanβ=16,求证:
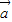 ∥
∥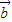 .
.
【答案】分析:(1)先根据向量的线性运算求出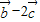 ,再由
,再由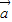 与
与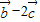 垂直等价于
垂直等价于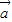 与
与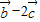 的数量积等于0可求出α+β的正余弦之间的关系,最后可求正切值.
的数量积等于0可求出α+β的正余弦之间的关系,最后可求正切值.
(2)先根据线性运算求出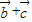 ,然后根据向量的求模运算得到|
,然后根据向量的求模运算得到|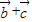 |的关系,最后根据正弦函数的性质可确定答案.
|的关系,最后根据正弦函数的性质可确定答案.
(3)将tanαtanβ=16化成弦的关系整理即可得到(4cosα)•(4cosβ)=sinαsinβ,正是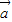 ∥
∥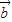 的充要条件,从而得证.
的充要条件,从而得证.
解答:解:(1)∵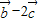 =(sinβ-2cosβ,4cosβ+8sinβ),
=(sinβ-2cosβ,4cosβ+8sinβ),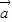 与
与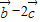 垂直,
垂直,
∴4cosα(sinβ-2cosβ)+sinα(4cosβ+8sinβ)=0,
即sinαcosβ+cosαsinβ=2(cosαcosβ-sinαsinβ),
∴sin(α+β)=2cos(α+β),∴tan(α+β)=2.
(2)∵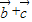 =(sinβ+cosβ,4cosβ-4sinβ),
=(sinβ+cosβ,4cosβ-4sinβ),
∴|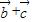 |=
|=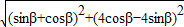
=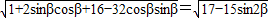 ,
,
∴当sin2β=-1时,|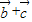 |取最大值,且最大值为
|取最大值,且最大值为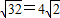 .
.
(3)∵tanαtanβ=16,∴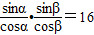 ,即sinαsinβ=16cosαcosβ,
,即sinαsinβ=16cosαcosβ,
∴(4cosα)•(4cosβ)=sinαsinβ,
即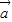 =(4cosα,sinα)与
=(4cosα,sinα)与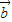 =(sinβ,4cosβ)共线,
=(sinβ,4cosβ)共线,
∴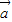 ∥
∥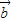 .
.
点评:本题主要考查向量的线性运算、求模运算、向量垂直和数量积之间的关系.向量和三角函数的综合题是高考的热点,要强化复习.
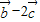 ,再由
,再由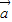 与
与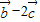 垂直等价于
垂直等价于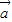 与
与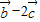 的数量积等于0可求出α+β的正余弦之间的关系,最后可求正切值.
的数量积等于0可求出α+β的正余弦之间的关系,最后可求正切值.(2)先根据线性运算求出
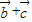 ,然后根据向量的求模运算得到|
,然后根据向量的求模运算得到|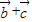 |的关系,最后根据正弦函数的性质可确定答案.
|的关系,最后根据正弦函数的性质可确定答案.(3)将tanαtanβ=16化成弦的关系整理即可得到(4cosα)•(4cosβ)=sinαsinβ,正是
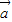 ∥
∥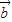 的充要条件,从而得证.
的充要条件,从而得证.解答:解:(1)∵
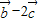 =(sinβ-2cosβ,4cosβ+8sinβ),
=(sinβ-2cosβ,4cosβ+8sinβ),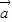 与
与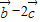 垂直,
垂直,∴4cosα(sinβ-2cosβ)+sinα(4cosβ+8sinβ)=0,
即sinαcosβ+cosαsinβ=2(cosαcosβ-sinαsinβ),
∴sin(α+β)=2cos(α+β),∴tan(α+β)=2.
(2)∵
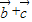 =(sinβ+cosβ,4cosβ-4sinβ),
=(sinβ+cosβ,4cosβ-4sinβ),∴|
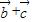 |=
|=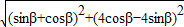
=
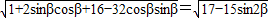 ,
,∴当sin2β=-1时,|
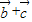 |取最大值,且最大值为
|取最大值,且最大值为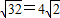 .
.(3)∵tanαtanβ=16,∴
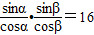 ,即sinαsinβ=16cosαcosβ,
,即sinαsinβ=16cosαcosβ,∴(4cosα)•(4cosβ)=sinαsinβ,
即
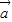 =(4cosα,sinα)与
=(4cosα,sinα)与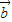 =(sinβ,4cosβ)共线,
=(sinβ,4cosβ)共线,∴
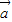 ∥
∥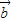 .
.点评:本题主要考查向量的线性运算、求模运算、向量垂直和数量积之间的关系.向量和三角函数的综合题是高考的热点,要强化复习.

练习册系列答案
相关题目


 与
与 垂直,求
垂直,求 的值;
的值;  的最大值; (3)若
的最大值; (3)若 ,判断
,判断 是平行还是垂直.
是平行还是垂直.
 与
与 垂直,求
垂直,求 的值;
的值; 的最大值;
的最大值; ,求证:
,求证: .
.
 与
与 垂直,求
垂直,求 的值;
的值;  的最大值;
的最大值; 
 (1)若
(1)若 与
与 垂直,求
垂直,求 的值;(2)求
的值;(2)求 的最大值;
的最大值;  ,求证:
,求证: . www.7caiedu.cn
. www.7caiedu.cn