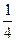题目内容

已知某随机变量ξ的概率分布列如表，其中x＞0，y＞0，随机变量ξ的方差Dξ=
1
2
，则x+y=______．
ξ123
PXyx
由题意可得：2x+y=1，Eξ=x+2y+3x=4x+2y=4x+2（1-2x）=2．
∴方差Dξ=
1
2
=（1-2）2x+（2-2）2（1-2x）+（3-2）2x．
化为2x=
1
2
，解得x=
1
4
，
∴y=1-2×
1
4
=
1
2
．
∴x+y=
1
4
+
1
2
=
3
4
．
故答案为
3
4
．
练习册系列答案
相关题目
（本小题满分12分）

2008年为山东素质教育年，为响应素质教育的实施，某中学号召学生在放假期间至少参加一次社会实践活动（以下简称活动）．现统计了该校100名学生参加活动的情况，他们参加活动的次数统计如图所示．
（1）求这些学生参加活动的人均次数；
（2）从这些学生中任选两名学生，求他们参加活动次数恰好相等的概率；
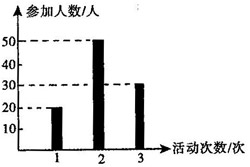
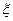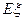（3）从这些学生中任选两名学生，用表示这两人参加活动次数之差的绝对值，求随机变量的分布列及数学期望．
某班共有学生40人，将一次数学考试成绩（单位：分）绘制成频率分布直方图，如图所示．
（Ⅰ）请根据图中所给数据，求出a的值；
（Ⅱ）从成绩在[50，70）内的学生中随机选3名学生，求这3名学生的成绩都在[60，70）内的概率；
（Ⅲ）为了了解学生本次考试的失分情况，从成绩在[50，70）内的学生中随机选取3人的成绩进行分析，用X表示所选学生成绩在[60，70）内的人数，求X的分布列和数学期望．
甲、乙两名同学参加一项射击游戏，两人约定，其中任何一人每射击一次，击中目标得2分，未击中目标得0分．若甲、乙两名同学射击的命中率分别为
3
5
和p，且甲、乙两人各射击一次所得分数之和为2的概率为
9
20
，假设甲、乙两人射击互不影响
（1）求p的值；
（2）记甲、乙两人各射击一次所得分数之和为ξ，求ξ的分布列和数学期望．
已知某一随机变量x的概率分布如下，且E（x）=5.9，则a的值为（　　）
x4a9
p0.50.2b
A．5B．6C．7D．8
设随机变量ξ的分布列如下：
ξ-101
Pabc
其中a，b，c成等差数列，若E（ξ）=
1
3
，则D（3ξ-1）=（　　）
A．4B．
5
3
C．
2
3
D．5
下图为某算法的程序框图，则程序运行后输出的结果是（   ）
A．2B．1C．3D．4
设离散型随机变量ξ满足Eξ=3，Dξ=1，则E[3（ξ-1）]等于（　　）
A．27B．24C．9D．6
已知ξ～B（n，p），且Eξ=7，Dξ=6，则p等于(     )
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网