题目内容
| ∫ | 1 -1 |
| 1-x2 |
| A、π | ||
B、
| ||
| C、π+1 | ||
| D、π-1 |
分析:先将
(
+x)dx拆分成
dx+∫-11xdx,利用几何意义求
dx的值,利用积分公式求∫-11xdx的值即可求出所求.
| ∫ | 1 -1 |
| 1-x2 |
| ∫ | 1 -1 |
| 1-x2 |
| ∫ | 1 -1 |
| 1-x2 |
解答:解:
(
+x)dx=
dx+∫-11xdx
=
+
x2|-11
=
故选:B
| ∫ | 1 -1 |
| 1-x2 |
| ∫ | 1 -1 |
| 1-x2 |
=
| π |
| 2 |
| 1 |
| 2 |
=
| π |
| 2 |
故选:B
点评:本题主要考查了定积分的几何意义,以及定积分的求解,同时考查了计算能力,属于基础题.

练习册系列答案
相关题目
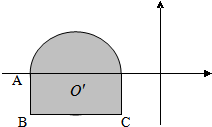 已知平面区域(含边界,上半部分为半圆,下半部分为矩形)如图,动点A(x,y)在该平面区域内,已知A(-3,0),C(-1,-1).
已知平面区域(含边界,上半部分为半圆,下半部分为矩形)如图,动点A(x,y)在该平面区域内,已知A(-3,0),C(-1,-1).