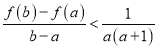题目内容
【题目】【2017届湖北省荆、荆、襄、宜四地七校考试联盟高三2月联考数学(文)】已知函数![]() .
.
(Ⅰ)讨论函数![]() 的极值点的个数;
的极值点的个数;
(Ⅱ)若![]() 有两个极值点
有两个极值点![]() ,证明:
,证明:![]() .
.
【答案】(Ⅰ)(ⅰ)![]()
![]()
![]() 时,
时,![]()
(ⅲ)当![]() 时,
时,![]()
【解析】试题分析:(Ⅰ)先求导数,再确定导函数零点情况,这需分类讨论:一次与二次的讨论,二次中有根与无根的讨论,两根情况分相等、一正一负、两不等正根,最后根据对应情况确定导函数符号变化规律,确定对应极值点个数;(Ⅱ)由(Ⅰ)先确定![]()
![]()
![]() 满足条件,再化简
满足条件,再化简![]() 为
为![]()
试题解析:解:(Ⅰ)由![]() 得,
得,
![]()
(ⅰ)![]()
![]() ,
,![]()
所以![]()
![]()
![]()
(ⅱ)![]()
![]()
![]() ,得
,得![]()
显然,![]() ,所以
,所以![]() ,
,
![]()
![]() 取得极小值,
取得极小值,![]()
(ⅲ)![]()
![]()
![]() 在
在![]()
![]()
当![]() 时,
时,![]()
![]() ,得
,得![]()
当![]() 和
和![]() 时
时![]() ,
,![]() 时,
时,![]() ,所以
,所以![]()
![]() 取得极小值,在
取得极小值,在![]() 取得极大值,所以
取得极大值,所以![]()
综上可知:(ⅰ)![]()
![]()
(ⅱ) 当![]() 时,
时,![]()
(ⅲ)当![]() 时,
时,![]()
(Ⅱ)由(Ⅰ)知,当且仅当![]() 时,
时,![]()
![]() 和极大值点
和极大值点![]() ,且
,且
![]() 是方程
是方程![]() 的两根,所以
的两根,所以![]() ,
,
![]()
![]()
![]() ,
,
设![]() ,
,![]() ,
,
所以![]() 时,
时,![]()
![]() ,则
,则![]()
所以![]() 得证.
得证.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某商场经营一批进价为![]() 元/台的小商品,经调查得知如下数据.若销售价上下调整,销售量和利润大体如下:
元/台的小商品,经调查得知如下数据.若销售价上下调整,销售量和利润大体如下:
销售价( |
|
|
|
|
日销售量( |
|
|
|
|
日销售额( |
| |||
日销售利润( |
|
(1)在下面给出的直角坐标系中,根据表中的数据描出实数对![]() 的对应点,并写出
的对应点,并写出![]() 与
与![]() 的一个函数关系式;
的一个函数关系式;
(2)请把表中的空格里的数据填上;
(3)根据表中的数据求![]() 与
与![]() 的函数关系式,并指出当销售单价为多少元时,才能获得最大日销售利润?
的函数关系式,并指出当销售单价为多少元时,才能获得最大日销售利润?