题目内容
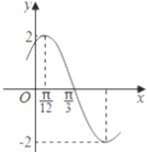
【题目】已知函数![]() 的部分图象如图所示.
的部分图象如图所示.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)将函数![]() 的图象做怎样的平移变换可以得到函数
的图象做怎样的平移变换可以得到函数![]() 的图象;
的图象;
(Ⅲ)若方程![]() 在
在![]() 上有两个不相等的实数根,求
上有两个不相等的实数根,求![]() 的取值范围.
的取值范围.
【答案】(I)![]() ;(II)沿
;(II)沿![]() 轴向左平移
轴向左平移![]() (III)
(III)![]()
【解析】试题分析:(Ⅰ)根据图象得A=2,T=π,故可得ω=2,所以f(x)=2sin(2x+φ),又点(![]() ,2)在函数的图象上,从而得到φ=
,2)在函数的图象上,从而得到φ=![]() ,所以
,所以![]() 。(Ⅱ)由于y= =2sin[2(x﹣
。(Ⅱ)由于y= =2sin[2(x﹣![]() )],f(x)=2sin[2(x﹣
)],f(x)=2sin[2(x﹣ ![]() +
+![]() )],因此可得将函数y=
)],因此可得将函数y=![]() sin2x﹣cos2x的图象沿x轴向左平移
sin2x﹣cos2x的图象沿x轴向左平移![]() 可以得到函数f(x)的图象。(Ⅲ)画出函数
可以得到函数f(x)的图象。(Ⅲ)画出函数![]() 在
在![]() 上图象,结合图象求解即可。
上图象,结合图象求解即可。
试题解析:
(1)根据图象得A=2,![]() =
=![]() ﹣
﹣![]() =
=![]() ,
,
∴T=π,
由![]() =π,可得ω=2,
=π,可得ω=2,
∴f(x)=2sin(2x+φ),
又点(![]() ,2)在函数的图象上,
,2)在函数的图象上,
∴2sin(![]() +φ)=2,
+φ)=2,
∵|φ|<![]() ,
,
∴φ=![]() ,
,
∴f(x)=2sin(2x+![]() ).
).
(2)∵y=![]() sin2x﹣cos2x=2sin(2x﹣
sin2x﹣cos2x=2sin(2x﹣![]() )=2sin[2(x﹣
)=2sin[2(x﹣![]() )],
)],
又f(x)=2sin(2x+![]() )=2sin[2(x+
)=2sin[2(x+![]() )]=2sin[2(x﹣
)]=2sin[2(x﹣ ![]() +
+![]() )],
)],
∴将函数y=![]() sin2x﹣cos2x的图象沿x轴向左平移
sin2x﹣cos2x的图象沿x轴向左平移![]() 可以得到函数f(x)的图象。
可以得到函数f(x)的图象。
(3)∵![]() ,
,
∴![]() 。
。
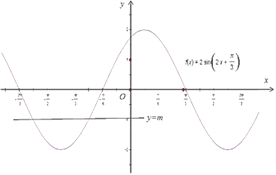
画出函数![]() 在
在![]() 上图象如图所示。
上图象如图所示。
结合函数的图象可得若方程f(x)=m在区间[﹣![]() ,0]内有两个不相等的实数根,
,0]内有两个不相等的实数根,
则![]() 。
。
∴要有两个不相等的实根,实数m的取值范围为![]() 。
。

练习册系列答案
相关题目