题目内容
观察式子:1+ <
< ,1+
,1+ +
+ <
< ,1+
,1+ +
+ +
+ <
< , ,则可归纳出一般式子为( )
, ,则可归纳出一般式子为( )
A.1+ + + + + + + < < (n≥2) (n≥2) | B.1+ + + + + + + < < (n≥2) (n≥2) |
C.1+ + + + + + + < < (n≥2) (n≥2) | D.1+ + + + + + + < < (n≥2) (n≥2) |
C
解析试题分析:根据题意,由于观察式子:1+ <
< ,1+
,1+ +
+ <
< ,1+
,1+ +
+ +
+ <
< ,左边是n个自然数平方的倒数和,右边是项数分之项数的二倍减去1,那么可得到,推广到一般1+
,左边是n个自然数平方的倒数和,右边是项数分之项数的二倍减去1,那么可得到,推广到一般1+ +
+ + +
+ + <
< (n≥2),故选C.
(n≥2),故选C.
考点:归纳推理
点评:主要是考查了归纳推理的基本运用,属于基础题。

练习册系列答案
相关题目
数学归纳法适用于证明的命题类型是
A.已知 结论 结论 | B.结论 已知 已知 | C.直接证明比较困难 | D.与正整数有关 |
下列表述正确的是
①归纳推理是由部分到整体的推理;②归纳推理是由一般到一般的推理;③演绎推理是由一般到特殊的推理;④类比推理是由特殊到一般的推理;⑤类比推理是由特殊到特殊的推理.
| A.①②③ | B.②③④ | C.②④⑤ | D.①③⑤ |
观察下列各式: =3125,
=3125, =15625,
=15625, =78125, ,则
=78125, ,则 的末四位数字为( )
的末四位数字为( )
| A.3125 | B.5625 | C.0625 | D.8125 |
用反证法证明某命题时,对其结论:“自然数 中恰有一个偶数”正确的反设为( )
中恰有一个偶数”正确的反设为( )
A. 都是奇数 都是奇数 |
B. 都是偶数 都是偶数 |
C. 中至少有两个偶数 中至少有两个偶数 |
D. 中至少有两个偶数或都是奇数 中至少有两个偶数或都是奇数 |
把1,3,6,10,15,21,…这些数叫做三角形数,这是因为这些数目的点子可以排成一个正三角形,则第七个三角形数是( )
| A.21 | B.28 | C.32 | D.36 |
如果△A1B1C1的三个内角的余弦值分别等于△A2B2C2的三个内角的正弦值,那么( )
| A.△A1B1C1和△A2B2C2都是锐角三角形 |
| B.△A1B1C1和△A2B2C2都是钝角三角形 |
| C.△A1B1C1是钝角三角形,△A2B2C2是锐角三角形 |
| D.△A1B1C1是锐角三角形,△A2B2C2是钝角三角形 |
 ,求出
,求出 猜想出数列的前n项和Sn的表达式
猜想出数列的前n项和Sn的表达式 的面积
的面积 ,猜想出椭圆
,猜想出椭圆 的面积
的面积
 ,且
,且 当
当 且
且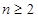 时,
时, 猜想
猜想 的表达式 .
的表达式 .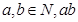 能被3整除,那么
能被3整除,那么 中至少有一个能被3整除"时,假设应为 .
中至少有一个能被3整除"时,假设应为 .