题目内容
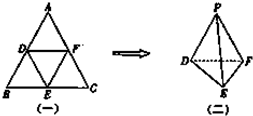 如图(一)等腰三角形ABC满足AB=AC=10,BC=12,D、E、F为AB、BC、AC的中点,现将△ADF、△BDE、△CEF分别沿DF、DE、EF折起使得A、B、C重合为一点P,形成一个三棱锥P-DEF如图(二),则三棱锥P-DEF的体积为( )
如图(一)等腰三角形ABC满足AB=AC=10,BC=12,D、E、F为AB、BC、AC的中点,现将△ADF、△BDE、△CEF分别沿DF、DE、EF折起使得A、B、C重合为一点P,形成一个三棱锥P-DEF如图(二),则三棱锥P-DEF的体积为( )分析:取DF的中点O,连接OE、OP,证明OP⊥DF,OE⊥DF,求得三角形POE的面积,即可求得三棱锥P-DEF的体积;
解答:解:折叠后的三棱锥如图:

其中PD=PF=5,PE=6,DF=6,DE=EF=5,
DF的中点O,连接OP、OE,有OP⊥DF,OE⊥DF,OD=3,
△POD中,PO=
=4,同理OE=4,

在等腰三角形POE中PE=6,PE边上的高h=
=
,
∴V=
×S△POE×DF=
×
×6×
×6=6
.
故选B.

其中PD=PF=5,PE=6,DF=6,DE=EF=5,
DF的中点O,连接OP、OE,有OP⊥DF,OE⊥DF,OD=3,
△POD中,PO=
| 52-32 |

在等腰三角形POE中PE=6,PE边上的高h=
| 42-32 |
| 7 |
∴V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 7 |
| 7 |
故选B.
点评:本题主要考查了棱锥的体积计算,考查空间想象能力、运算能力和推理论证能力,解题的关键是利用等体积转化,利用平面几何知识求数据.

练习册系列答案
相关题目
 (三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)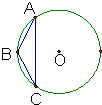 (2013•珠海一模)(几何证明选讲选做题)
(2013•珠海一模)(几何证明选讲选做题) 为一个等腰三角形形状的空地,腰
为一个等腰三角形形状的空地,腰 的长为
的长为 (百米),底
(百米),底 的长为
的长为 (百米).现决定在空地内筑一条笔直的小路
(百米).现决定在空地内筑一条笔直的小路 (宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等、面积分别为
(宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等、面积分别为 和
和 .
.
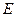 为
为 的中点,求此时小路的长度;
的中点,求此时小路的长度; 的最小值.
的最小值. 为一个等腰三角形形状的空地,腰
为一个等腰三角形形状的空地,腰 的长为
的长为 (百米),底
(百米),底 的长为
的长为 (百米).现决定在空地内筑一条笔直的小路
(百米).现决定在空地内筑一条笔直的小路 (宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等、面积分别为
(宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等、面积分别为 和
和 .
.
 为
为 的中点,求此时小路的长度;
的中点,求此时小路的长度; 的最小值.
的最小值.