Question

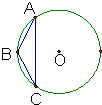
（2013•珠海一模）（几何证明选讲选做题）
如图所示，等腰三角形ABC的底边AC长0为6，其外接圆的半径长为5，则三角形ABC的面积是

3

．

Answer 1

分析：根据等腰三角形ABC的底边AC长为6，其外接圆的半径长为5，由勾股定理可知弦心距，对于三角形已知高和对应的边长，求出面积．

解答：解：∵等腰三角形ABC的底边AC长为6，其外接圆的半径长为5
∴半径，弦心距和弦长组成一个直角三角形，有勾股定理可知弦心距是

52-32

=4，
∴三角形的高是5-4=1，
∴三角形的面积是

1

2

×1×6=3，
故答案为：3．

点评：本题考查三角形的面积公式，是一个基础题，解题的关键是构造直角三角形，在圆中这个直角三角形是经常用来求解线段的长度的．