题目内容
直线xcosθ+ysinθ+a=0与xsinθ-ycosθ+b=0的位置关系是（ ）A．平行
B．垂直
C．斜交
D．与a，b，θ的值有关
【答案】分析：当这两条直线中有一条斜率不存在时，检验他们的位置关系式垂直关系．当它们的斜率都存在时，求出他们的斜率，
发现斜率之积等于-1，两条直线垂直．
解答：解：当cosθ=0或sinθ=0时，这两条直线中，有一条斜率为0，另一条斜率不存在，两条直线垂直．
当cosθ和sinθ都不等于0时，这两条直线的斜率分别为-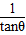
和tanθ，显然，斜率之积等于-1，
故两直线垂直．综上，两条直线一定是垂直的关系，
故选 B．
点评：本题考查两条直线垂直的条件是斜率之积等于-1，或者它们的斜率中一个等于0，而另一个不存在．体现了分类讨论的数学思想．
发现斜率之积等于-1，两条直线垂直．
解答：解：当cosθ=0或sinθ=0时，这两条直线中，有一条斜率为0，另一条斜率不存在，两条直线垂直．
当cosθ和sinθ都不等于0时，这两条直线的斜率分别为-
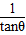和tanθ，显然，斜率之积等于-1，故两直线垂直．综上，两条直线一定是垂直的关系，
故选 B．
点评：本题考查两条直线垂直的条件是斜率之积等于-1，或者它们的斜率中一个等于0，而另一个不存在．体现了分类讨论的数学思想．
练习册系列答案
相关题目
已知向量
=（2cosα，2sinα），
=（3cosβ，3sinβ），若向量
与
的夹角为60°，则直线xcosα-ysinα+
=0与圆(x-cosβ)2+(y+sinβ)2=
的位置关系是（ ）
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| 1 |
| 2 |
| A、相交 | B、相切 |
| C、相离 | D、相交且过圆心 |
直线xcosθ+ysinθ+a=0与xsinθ-ycosθ+b=0的位置关系是（ ）
| A、平行 | B、垂直 | C、斜交 | D、与a，b，θ的值有关 |