题目内容
函数y＝
(x2－4x＋3)的单调递增区间为( )
(x2－4x＋3)的单调递增区间为( )| A．(3，＋∞) | B．(－∞，1) |
| C．(－∞，1)∪(3，＋∞) | D．(0，＋∞) |
B
令u＝x2－4x＋3，原函数可以看作y＝u与u＝x2－4x＋3的复合函数．
令u＝x2－4x＋3>0，
则x<1或x>3.
∴函数y＝(x2－4x＋3)的定义域为(－∞，1)∪(3，＋∞)．
又u＝x2－4x＋3的图象的对称轴为x＝2，且开口向上，
∴u＝x2－4x＋3在(－∞，1)上是减函数，在(3，＋∞)上是增函数．而函数y＝u在(0，＋∞)上是减函数，
∴y＝(x2－4x＋3)的单调递减区间为(3，＋∞)，单调递增区间为(－∞，1)．
u与u＝x2－4x＋3的复合函数．令u＝x2－4x＋3>0，
则x<1或x>3.
∴函数y＝
(x2－4x＋3)的定义域为(－∞，1)∪(3，＋∞)．又u＝x2－4x＋3的图象的对称轴为x＝2，且开口向上，
∴u＝x2－4x＋3在(－∞，1)上是减函数，在(3，＋∞)上是增函数．而函数y＝
u在(0，＋∞)上是减函数，∴y＝
(x2－4x＋3)的单调递减区间为(3，＋∞)，单调递增区间为(－∞，1)．
练习册系列答案
智能训练练测考系列答案
相关题目
，
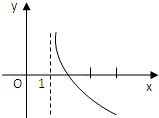
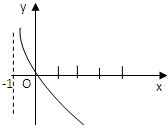
的图象可能是（ ）
，则( )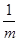
＋
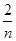的最小值为________．
，两边求导数得
＝
，于是y′＝f(x)g(x)·
的一个单调递增区间为( )．
= .
．