题目内容
设a=lg e,b=(lg e)2,c=lg ,则( )
,则( )
 ,则( )
,则( )| A.a>b>c | B.a>c>b |
| C.c>a>b | D.c>b>a |
B
∵1<e<3,则1< <e<e2<10.
<e<e2<10.
∴0<lg e<1.则lg =
=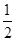 lg e<lg e,
lg e<lg e,
即c<a.又0<lg e<1,
∴(lg e)2<lg e,即b<a.同时c-b=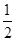 lg e-(lg e)2=
lg e-(lg e)2=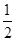 lg e(1-2 lg e)=
lg e(1-2 lg e)=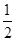 lg e·lg
lg e·lg >0.
>0.
∴c>b.故应选B.
 <e<e2<10.
<e<e2<10.∴0<lg e<1.则lg
 =
=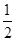 lg e<lg e,
lg e<lg e,即c<a.又0<lg e<1,
∴(lg e)2<lg e,即b<a.同时c-b=
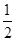 lg e-(lg e)2=
lg e-(lg e)2=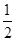 lg e(1-2 lg e)=
lg e(1-2 lg e)=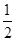 lg e·lg
lg e·lg >0.
>0.∴c>b.故应选B.

练习册系列答案
相关题目

 其中
其中 且
且 .
. ,求
,求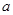 的值;
的值; 上
上 恒成立,求
恒成立,求 (
( 且
且 )满足
)满足 ,则
,则 的解为( )
的解为( )

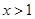

 (x2-4x+3)的单调递增区间为( )
(x2-4x+3)的单调递增区间为( )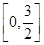 上的最大值.
上的最大值. ,若
,若 且
且 ,则
,则 的取值范围是
的取值范围是  ,且
,且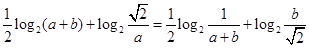 ,则
,则 ( )
( )