题目内容
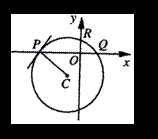
圆C通过不同三点P(k,0)、Q(2,0)、R(0,1),已知圆C在点P的切线的斜率为1,试求圆C的方程.
[解析] 设圆C的方程为x2+y2+Dx+Ey+F=0,
∵点P(k,0)、Q(2,0)在圆上,
∴k、2为方程x2+Dx+F=0的两根.
∴k+2=-D,2k=F.即![]() ,
,
又因圆过点P(0,1),故1+E+F=0.
∴E=-F-1=-2k-1,故圆的方程为
x2+y2-(k+2)x-(2k+1)y+2k=0.
∴圆心C的坐标为![]() .
.
又∵圆在点P的切线斜率为1,
∴![]() =-1,即k=-3,
=-1,即k=-3,
从而D=1,E=5,F=-6.
即圆的方程为x2+y2+x+5y-6=0.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目