题目内容
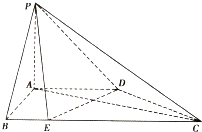
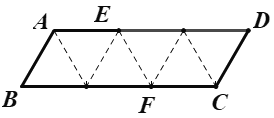
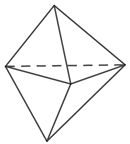
【题目】如图，平行四边形形状的纸片是由六个边长为1的正三角形构成的，将它沿虚线折起来，可以得到如图所示粽子形状的六面体，则该六面体的表面积为__________；若该六面体内有一小球，则小球的最大体积为___________．
【答案】
【解析】
（1）计算每个面的面积再乘以6，即可得到答案；
（2）由图形的对称性得，小球的体积要达到最大，即球与六个面都相切时，求出球的半径
，再代入球的体积公式可得答案.
（1）因为
，所以该六面体的表面积为.
（2）由图形的对称性得，小球的体积要达到最大，即球与六个面都相切时，
每个三角形面积是
，六面体体积是正四面体的2倍，所以六面体体积是
.
由于图像的对称性，内部的小球要是体积最大，就是球要和六个面相切，连接球心和五个顶点，把六面体分成了六个三棱锥，设球的半径为，
所以
，
所以球的体积
.
故答案为： ；.
练习册系列答案
相关题目
