题目内容
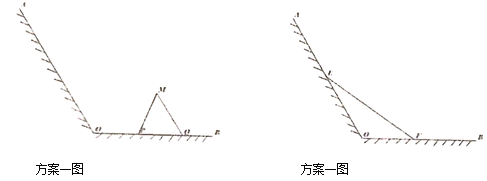
【题目】江心洲有一块如图所示的江边，
，
为岸边，岸边形成
角，现拟在此江边用围网建一个江水养殖场，有两个方案：方案l：在岸边上取两点
，用长度为
的围网依托岸边线
围成三角形
（
，
两边为围网）；方案2：在岸边，上分别取点
，用长度为的围网
依托岸边围成三角形
.请分别计算
，
面积的最大值，并比较哪个方案好.
【答案】
，
面积的最大值分别为
，
.其中方案
好.
【解析】
分别在三角形面积公式中应用基本不等式、余弦定理中利用基本不等式计算出方案
和方案中
和面积的最大值，通过最大值的比较可知方案好.
方案：设
，
由已知“用长度为
的围网，
，
两边为围网”得
且
当且仅当
且
时，等号成立
面积的最大值为
方案：设
，
在中，由余弦定理得：
即
（当且仅当
时等号成立）
（当且仅当时等号成立）
面积的最大值为
方案好
练习册系列答案
相关题目
