题目内容
已知定义在![]() 上的函数
上的函数![]() 满足条件:对于任意的
满足条件:对于任意的![]() ,都有
,都有![]() .当
.当![]() 时,
时,![]() .
.
(1)求证:函数![]() 是奇函数;
是奇函数;
(2)求证:函数![]() 在
在![]() 上是减函数;
上是减函数;
(3)解不等式![]() .
.
(1)证明:令![]() ,则
,则![]() ,得
,得![]() .
.
令![]() ,则
,则![]() ,即
,即![]() .故函数
.故函数![]() 是奇函数.
是奇函数.
(2)证明:对于![]() 上的任意两个值
上的任意两个值![]() ,
,![]() ,且
,且![]() ,
,
则![]() ,
,
又![]() ,则
,则![]() ,又当
,又当![]() 时,
时,![]() .
.
![]()
![]() , 即
, 即![]() .故函数
.故函数![]() 在
在![]() 上是减函数.
上是减函数.
(3)解:由(2)知:函数![]() 在R上是减函数.
在R上是减函数.
![]() ,
,![]() .
.
![]() ,解得
,解得![]() .又
.又![]() 所以解集为
所以解集为![]() .
.

练习册系列答案
相关题目
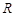 上的函数
上的函数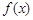 满足
满足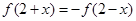 ,当
,当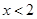 时,
时,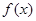 单调递增,若
单调递增,若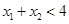 且
且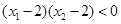 ,则
,则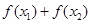 的值( )
的值( )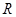 上的函数
上的函数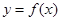 满足下列条件:①对任意的
满足下列条件:①对任意的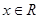 都有
都有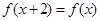 ;②若
;②若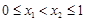 ,都有
,都有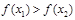 ;③
;③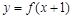 是偶函数,则下列不等式中正确的是()
是偶函数,则下列不等式中正确的是()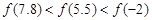 B、
B、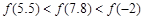
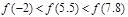 D、
D、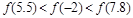
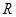 上的函数
上的函数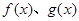 满足
满足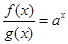 ,
,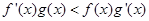 ,
, 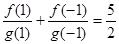 ,有穷数列
,有穷数列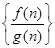 (
(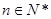 )的前
)的前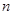 项和等于
项和等于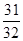 , 则n等于
, 则n等于