题目内容
在直角坐标系xOy中,点P(xP,yP)和点Q(xQ,yQ)满足 按此规则由点P得到点Q,称为直角坐标平面的一个“点变换”.此变换下,若
按此规则由点P得到点Q,称为直角坐标平面的一个“点变换”.此变换下,若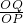 =m,∠POQ=θ,其中O为坐标原点,则y=msin(x+θ)的图象在y轴右边第一个最高点的坐标为________.
=m,∠POQ=θ,其中O为坐标原点,则y=msin(x+θ)的图象在y轴右边第一个最高点的坐标为________.
( ,
, )
)
分析:先利用两点间的距离公式及已知的点变换公式,计算m的值,再利用向量夹角公式和点变换公式计算∠POQ=θ 的值,最后利用三角函数的图象和性质,得函数的最高点坐标即可
解答:依题意,(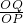 )2=
)2= =m2
=m2
∵
∴ =m2
=m2
∴ =m2
=m2
∴m2=2,
即m=
∵∠POQ=θ,
∴cosθ= =
= =
= =
= =
=
∵θ=
∴函数y=msin(x+θ)即为y= sin(x+
sin(x+ )
)
∴此函数在y轴右边第一个最高点的坐标为( ,
, )
)
故答案为( ,
, )
)
点评:本题综合考察了理解题意的能力,两点间的距离公式,向量夹角公式,具有较强的代数变换能力是解决本题的关键
 ,
, )
)分析:先利用两点间的距离公式及已知的点变换公式,计算m的值,再利用向量夹角公式和点变换公式计算∠POQ=θ 的值,最后利用三角函数的图象和性质,得函数的最高点坐标即可
解答:依题意,(
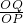 )2=
)2= =m2
=m2∵

∴
 =m2
=m2∴
 =m2
=m2∴m2=2,
即m=

∵∠POQ=θ,
∴cosθ=
 =
= =
= =
= =
=
∵θ=

∴函数y=msin(x+θ)即为y=
 sin(x+
sin(x+ )
)∴此函数在y轴右边第一个最高点的坐标为(
 ,
, )
)故答案为(
 ,
, )
)点评:本题综合考察了理解题意的能力,两点间的距离公式,向量夹角公式,具有较强的代数变换能力是解决本题的关键

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,在直角坐标系xOy中,射线OA在第一象限,且与x轴的正半轴成定角60°,动点P在射线OA上运动,动点Q在y轴的正半轴上运动,△POQ的面积为
如图所示,在直角坐标系xOy中,射线OA在第一象限,且与x轴的正半轴成定角60°,动点P在射线OA上运动,动点Q在y轴的正半轴上运动,△POQ的面积为