题目内容
如图，经过正三棱柱底面一边AB，作与底面成30角的平面，已知截面三角形ABD的面积为32cm2，求截得的三棱锥D-ABC的体积．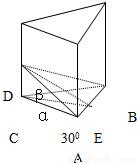
【答案】分析：作△ABC的高CE，连接DE，利用截面三角形ABD的面积为32cm2，求出底面棱长，三棱锥的高CD，求出底面面积，再求它的体积．
解答：解：因为这个三棱锥是正三棱锥，
所以△ABC是正三角形，
且DC所在直线与△ABC所在平面垂直
如图，作△ABC的高CE，连接DE
由三垂线定理，知DE⊥AB，所以
∠DEC是二面角α-AB-β的平面角，∠DEC=30°
CE=
用S截表示△ABD的面积，
则32=S截=
，
∴AB=8．
用S底表示△ABC的面积，则
S底=
．
∵∠DEC=30°，所以DC=4，
∴V三棱锥=
S底•DC=
．
点评：本题考查棱柱、棱锥、棱台的体积，考查逻辑思维能力，计算能力，是基础题．
解答：解：因为这个三棱锥是正三棱锥，
所以△ABC是正三角形，
且DC所在直线与△ABC所在平面垂直
如图，作△ABC的高CE，连接DE
由三垂线定理，知DE⊥AB，所以
∠DEC是二面角α-AB-β的平面角，∠DEC=30°
CE=
用S截表示△ABD的面积，
则32=S截=
，∴AB=8．
用S底表示△ABC的面积，则
S底=
．∵∠DEC=30°，所以DC=4，
∴V三棱锥=
S底•DC=．点评：本题考查棱柱、棱锥、棱台的体积，考查逻辑思维能力，计算能力，是基础题．
练习册系列答案
相关题目
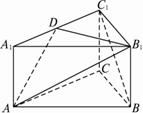
已知（如图）在正三棱柱（底面正三角形，侧棱垂直于底面）ABC-A1B1C1中，若AB=AA1=4，点D是AA1的中点，点P是BC1中点
,若经过对角线AB1且与对角线BC1平行的平面交上底面一边A1C1于点D.
