题目内容

已知F1，F2分别是双曲线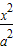-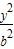=1（a＞0，b＞0）的左、右焦点，过F1且垂直于x轴的直线与双曲线交于A，B两点，若△ABF2是直角三角形，则该双曲线离心率的值等于（ ）
A．
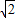
B．1+
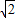
C．
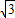
D．3
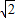
【答案】分析：利用双曲线的性质和等腰直角三角形的性质、离心率计算公式即可得出．
解答：解：设A（-c，y），由题意可得，解得．
∵△ABF2是直角三角形，∴，∴2ac=c2-a2，
化为e2-2e-1=0，解得．
故选B．
点评：熟练掌握双曲线的性质和等腰直角三角形的性质、离心率计算公式是解题的关键．
练习册系列答案
相关题目
（2013•湖南）已知F1，F2分别是椭圆E：
x25
+y2=1的左、右焦点F1，F2关于直线x+y-2=0的对称点是圆C的一条直径的两个端点．
（Ⅰ）求圆C的方程；
（Ⅱ）设过点F2的直线l被椭圆E和圆C所截得的弦长分别为a，b．当ab最大时，求直线l的方程．
（2013•青岛二模）已知F1、F2分别是双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的左、右焦点，P为双曲线右支上的一点，
PF2
⊥
F1F2
，且|
PF1
|=
2
|
PF2
|，则双曲线的离心率为（　　）
已知F1，F2分别是双曲线
x2
a2
-
y2
b2
=1 (a＞0， b＞0)的左、右焦点，过点F2与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M，若点M在以线段F1F2为直径的圆外，则双曲线离心率的取值范围是（　　）
如图，已知F1，F2分别是椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点，且椭圆C的离心率e=
1
2
，F1也是抛物线C1：y2=-4x的焦点．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过点F2的直线l交椭圆C于D，E两点，且2
DF2
=
F2E
，点E关于x轴的对称点为G，求直线GD的方程．
已知F1，F2分别是双曲线
x2
a2
-
y2
b2
=1(a＞0，b＞0)的左，右焦点，P是双曲线的上一点，若
PF1
•
PF2
=0且|
PF1
|•|
PF2
|=3ab，则双曲线的离心率是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网