Question

解不等式:(x²-1)(x²-5x+6)≥0.

   

Answer 1

思路分析:高次不等式中x²-1与x²-5x+6两个因式都是一元二次式,因此可化为不等式组来求解,当然也可用数轴标根法.

解法一:(x²-1)(x²-5x+6)≥0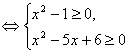  ①

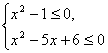或                                            ②

    不等式组①的解集为{x|x≤-1或1≤x≤2或x≥3}.

    不等式组②的解集为.

∴原不等式的解集为{x|x≤-1或1≤x≤2或x≥3}.

    解法二:将原不等式化为(x+1)(x-1)(x-2)(x-3)≥0,对应方程的各根依次为-1,1,2,3,将其标在数轴上(如下图),穿线如图:

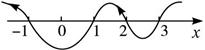
    由数轴标根法得原不等式的解集为{x|x≤-1或1≤x≤2或x≥3}.