题目内容
用定义法证明函数f(x)=
在(-2,+∞)上是单调减函数.
| x+3 | 3x+6 |
分析:设-2<x1<x2,变形为f(x)=
=
+
,通过作差f(x1)-f(x2)并判断其符号即可.
| x+2+1 |
| 3(x+2) |
| 1 |
| 3 |
| 1 |
| 3(x+2) |
解答:解:设-2<x1<x2,
∵f(x)=
=
+
∴f(x1)-f(x2)=[
+
]-[
+
]=
,
又∵-2<x1<x2,
∴
>0,
∴f(x1)>f(x2),
∴f(x)=
在(-2,+∞)上是单调减函数.
∵f(x)=
| x+2+1 |
| 3(x+2) |
| 1 |
| 3 |
| 1 |
| 3(x+2) |
∴f(x1)-f(x2)=[
| 1 |
| 3 |
| 1 |
| 3(x1+2) |
| 1 |
| 3 |
| 1 |
| 3(x2+2) |
| x2-x1 |
| 3(x1+2)(x2+2) |
又∵-2<x1<x2,
∴
| x2-x1 |
| 3(x1+2)(x2+2) |
∴f(x1)>f(x2),
∴f(x)=
| x+3 |
| 3x+6 |
点评:本题考查了用定义法证明函数的单调性,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 在x∈[2,+∞)上是增函数;
在x∈[2,+∞)上是增函数;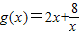 在[4,8]上的值域.
在[4,8]上的值域.