题目内容
设
(1)如果 在
在 处取得最小值
处取得最小值 ,求
,求 的解析式;
的解析式;
(2)如果 ,
, 的单调递减区间的长度是正整数,试求
的单调递减区间的长度是正整数,试求 和
和 的值.(注:区间
的值.(注:区间 的长度为
的长度为 )
)
【答案】
(1)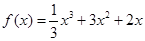 ;(2)
;(2)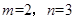 或
或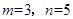
【解析】
试题分析:(1)由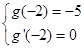 可求解
可求解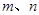 的值,进而的函数
的值,进而的函数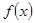 的解析式;(2)由
的解析式;(2)由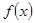 的单调递减区间得
的单调递减区间得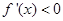 ,再用
,再用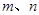 表示出区间
表示出区间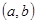 的长度为
的长度为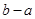 ,代入数值验证即可求得
,代入数值验证即可求得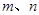 的值
的值
试题解析:(1)已知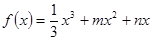 ,
,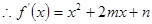
又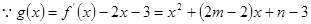 在
在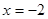 处取极值,
处取极值,
则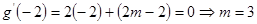 ,又在
,又在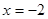 处取最小值-5
处取最小值-5
则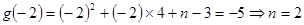 ,
,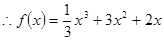
(2)要使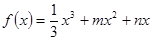 单调递减,则
单调递减,则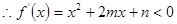
又递减区间长度是正整数,所以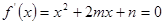 两根设做a,b。即有:
两根设做a,b。即有:
b-a为区间长度。又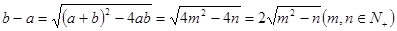
又b-a为正整数,且m+n<10,所以m=2,n=3或,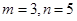 符合
符合
考点:1 函数的极值;2 函数的单调性

练习册系列答案
相关题目
 .
. 在
在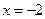 处取得最小值
处取得最小值 ,求
,求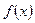 的解析式;
的解析式;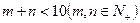 ,
,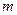 和
和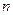
 的长度为
的长度为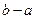 )
) .
. 在
在 处取得最小值
处取得最小值 ,求
,求 的解析式;
的解析式; ,
, 和
和
 的长度为
的长度为 )
) .
. 在
在 处取得最小值
处取得最小值 ,求
,求 的解析式;
的解析式; ,
, 和
和
 的长度为
的长度为 )
)