题目内容
设函数f(x)(x∈R)满足f(-x)=f(x),f(x)=f(2-x),且当x∈[0,1]时,f(x)=x3,又函数g(x)=|xcos(πx)|,则函数h(x)=g(x)-f(x)在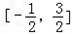 上的零点个数为
上的零点个数为
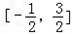 上的零点个数为
上的零点个数为[ ]
A.5
B.6
C.7
D.8
B.6
C.7
D.8
B

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
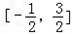 上的零点个数为
上的零点个数为
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案