题目内容
(理)等差数列{an}中,则a3+a4+a5=12,则4a3+2a6= ,若数列{bn}为等比数列,其前n项和Sn,若对任意n∈N*,点(n,Sn)均在函数y=bx+r(b>0且b≠1,b,r为常数)图象上,则r= .
【答案】分析:根据等差数列的性质得出a3+a5=2a4从而求出a4,再由4a3+2a6=4(a1+2d)+2(a1+5d)=6a1+18d=6a4,将相应的值的代入即可求出答案.
由已知得 Sn=bn+r,利用数列中an与 Sn关系 求{an}的通项公式,再据定义求出r的值.
求{an}的通项公式,再据定义求出r的值.
解答:解:等差数列{an}中,
∵a3+a4+a5=12,
∴a4=a1+3d=4,
∴4a3+2a6=4(a1+2d)+2(a1+5d)
=6a1+18d
=24.
因为对任意的n∈N*,点(n,Sn),
均在函数y=bx+r(b>0且b≠1,b,r均为常数)的图象上
所以得Sn=bn+r,
当n=1时,a1=S1=b+r,
当n≥2时,an=Sn-Sn-1=bn+r-(bn-1+r )=(b-1)b n-1,
又因为{an}为等比数列,
∴公比为b,
所以 ,
,
解得r=-1.
点评:此题第一小题考查学生灵活运用等差数列的前n项和公式化简求值,掌握等差数列的性质,是一道基础题.本题第二小题是函数与数列、不等式的综合.主要考查等比数列定义,及利用错位相消法来处理数列求和、恒成立问题.
由已知得 Sn=bn+r,利用数列中an与 Sn关系
 求{an}的通项公式,再据定义求出r的值.
求{an}的通项公式,再据定义求出r的值.解答:解:等差数列{an}中,
∵a3+a4+a5=12,
∴a4=a1+3d=4,
∴4a3+2a6=4(a1+2d)+2(a1+5d)
=6a1+18d
=24.
因为对任意的n∈N*,点(n,Sn),
均在函数y=bx+r(b>0且b≠1,b,r均为常数)的图象上
所以得Sn=bn+r,
当n=1时,a1=S1=b+r,
当n≥2时,an=Sn-Sn-1=bn+r-(bn-1+r )=(b-1)b n-1,
又因为{an}为等比数列,
∴公比为b,
所以
 ,
,解得r=-1.
点评:此题第一小题考查学生灵活运用等差数列的前n项和公式化简求值,掌握等差数列的性质,是一道基础题.本题第二小题是函数与数列、不等式的综合.主要考查等比数列定义,及利用错位相消法来处理数列求和、恒成立问题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
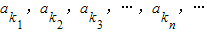 成等比数列,其中k1=1,k2=2,k3=5.
成等比数列,其中k1=1,k2=2,k3=5.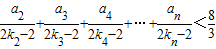 .
.