题目内容
已知方程x2-8x+6lnx-m=0有三个不同的实数解,则实数m范围为 .
【答案】分析:遇到方程根的问题,一般是构造新函数,题目转化为研究函数的零点问题,通过导数得到函数的最值,把函数的最值同0进行比较,得到结果.
解答:解:方程x2-8x+6lnx-m=0有三个不同的实数解
则函数m(x)=x2-8x+6lnx-m的图象与x轴的正半轴有且只有三个不同的交点.
∵m(x)=x2-8x+6lnx-m,
∴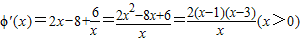 ,
,
当x∈(0,1)时,m'(x)>0,m(x)是增函数;
当x∈(0,3)时,m'(x)<0,m(x)是减函数;
当x∈(3,+∞)时,m'(x)>0,m(x)是增函数;
当x=1,或x=3时,m'(x)=0.
∴m(x)最大值=m(1)=-m-7,m(x)最小值=m(3)=-m+6ln3-15.
∵当x充分接近0时,m(x)<0,当x充分大时,m(x)>0.
∴要使m(x)的图象与x轴正半轴有三个不同的交点,必须且只须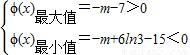
即6ln3-15<m<-7.
故答案为:6ln3-15<m<-7
点评:本小题主要考查函数的单调性、极值、最值等基本知识,考查运用导数研究函数性质的方法,考查运算能力,考查函数与方程、数形结合、分类与整合等数学思想方法和分析问题、解决问题的能力.
解答:解:方程x2-8x+6lnx-m=0有三个不同的实数解
则函数m(x)=x2-8x+6lnx-m的图象与x轴的正半轴有且只有三个不同的交点.
∵m(x)=x2-8x+6lnx-m,
∴
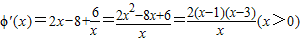 ,
,当x∈(0,1)时,m'(x)>0,m(x)是增函数;
当x∈(0,3)时,m'(x)<0,m(x)是减函数;
当x∈(3,+∞)时,m'(x)>0,m(x)是增函数;
当x=1,或x=3时,m'(x)=0.
∴m(x)最大值=m(1)=-m-7,m(x)最小值=m(3)=-m+6ln3-15.
∵当x充分接近0时,m(x)<0,当x充分大时,m(x)>0.
∴要使m(x)的图象与x轴正半轴有三个不同的交点,必须且只须
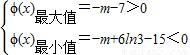
即6ln3-15<m<-7.
故答案为:6ln3-15<m<-7
点评:本小题主要考查函数的单调性、极值、最值等基本知识,考查运用导数研究函数性质的方法,考查运算能力,考查函数与方程、数形结合、分类与整合等数学思想方法和分析问题、解决问题的能力.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
已知抛物线y2=8x的准线与双曲线
-
=1(a>0,b>0)相交于A,B两点,双曲线的一条渐近线方程是y=2
x,点F是抛物线的焦点,且△FAB是直角三角形,则双曲线的标准方程是( )
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
A、
| ||||
B、x2-
| ||||
C、
| ||||
D、
|