题目内容
【题目】(本小题满分12分)设函数![]() .
.
(Ⅰ)讨论函数![]() 的单调性;
的单调性;
(Ⅱ)如果对所有的![]() ≥0,都有
≥0,都有![]() ≤
≤![]() ,求
,求![]() 的最小值;
的最小值;
(Ⅲ)已知数列![]() 中,
中, ![]() ,且
,且![]() ,若数列
,若数列![]() 的前n项和为
的前n项和为![]() ,求证:
,求证:
![]() .
.
【答案】(Ⅰ)函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 单调递增;(Ⅱ)
单调递增;(Ⅱ)![]() ;(Ⅲ)证明见解析.
;(Ⅲ)证明见解析.
【解析】试题(Ⅰ)先对函数![]() 求导,再对
求导,再对![]() 的取值范围进行讨论,即可得
的取值范围进行讨论,即可得![]() 的单调性;(Ⅱ)设
的单调性;(Ⅱ)设![]() ,先对函数
,先对函数![]() 求导,再对
求导,再对![]() 的取值范围进行讨论函数
的取值范围进行讨论函数![]() 的单调性,进而可得
的单调性,进而可得![]() 的最小值;(Ⅲ)先由已知条件求出数列
的最小值;(Ⅲ)先由已知条件求出数列![]() 的通项公式和前
的通项公式和前![]() 项和,再把
项和,再把![]() 转化为
转化为![]() ,由(Ⅱ)可得
,由(Ⅱ)可得![]() ,
, ![]() ,令
,令![]() ,可得
,可得![]() ,进而可证
,进而可证![]() ,即可证
,即可证![]() .
.
试题解析:(Ⅰ) ![]() 的定义域为
的定义域为![]() ,
, 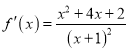 1分
1分
当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() 2分
2分
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 单调递增. 3分
单调递增. 3分
(Ⅱ)设![]() ,则
,则
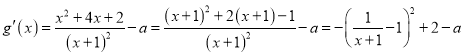
因为![]() ≥0,故
≥0,故![]() 5分
5分
(ⅰ)当![]() 时,
时, ![]() ,
, ![]() ,所以
,所以![]() 在
在![]() 单调递减,而
单调递减,而![]() ,所以对所有的
,所以对所有的![]() ≥0,
≥0, ![]() ≤0,即
≤0,即![]() ≤
≤![]() ;
;
(ⅱ)当![]() 时,
时, ![]() ,若
,若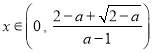 ,则
,则![]() ,
, ![]() 单调递增,而
单调递增,而![]() ,所以当
,所以当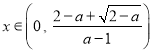 时,
时, ![]() ,即
,即![]() ;
;
(ⅲ)当![]() 时,
时, ![]() ,
, ![]() ,所以
,所以![]() 在
在![]() 单调递增,而
单调递增,而![]() ,所以对所有的
,所以对所有的![]() ,
, ![]() ,即
,即![]() ;
;
综上, ![]() 的最小值为2. 8分
的最小值为2. 8分
(Ⅲ)由![]() 得,
得, ![]() ,由
,由![]() 得,
得, ![]() ,
,
所以![]() ,数列
,数列![]() 是以
是以![]() 为首项,1为公差的等差数列,
为首项,1为公差的等差数列,
故![]() ,
, ![]() ,
, ![]() 9分
9分
![]()
![]()
![]()
由(Ⅱ)知![]() 时,
时, ![]() ,
, ![]() ,
,
即![]() ,
, ![]() . 10分
. 10分
法一:令![]() ,得
,得![]() ,
,
即![]()
因为![]() 11分
11分
所以![]() 12分
12分
故![]() 12分
12分
法二:
![]()
![]()
![]()
下面用数学归纳法证明.
(1)当![]() 时,令
时,令![]() 代入
代入![]() ,即得
,即得![]() ,不等式成立
,不等式成立
(2)假设![]() 时,不等式成立,即
时,不等式成立,即![]()
则![]() 时,
时, ![]()
令![]() 代入
代入![]() ,得
,得![]()
![]()
![]()
即![]()
由(1)(2)可知不等式![]() 对任何
对任何![]()
![]() 都成立.
都成立.
故![]() 12分
12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目