题目内容
已知数列{an}中,a1=3,点(an,an+1)在直线y=x+2上。
(1)求数列{an}的通项公式;
(2)若bn=an·3n,求数列{bn}的前n项和Tn。
解:(1)∵点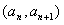 在直线y=x+2上
在直线y=x+2上
∴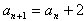 ,即
,即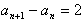
∴数列{an}是以3为首项,以2为公差的等差数列,
∴an=3+2(n-1)=2n+1。
(2)∵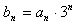
∴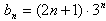
∴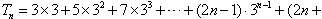 1)·3n ①
1)·3n ①
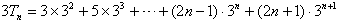 ②
②
由①-②得
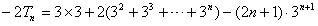
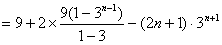
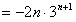
∴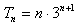 。
。
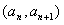 在直线y=x+2上
在直线y=x+2上∴
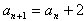 ,即
,即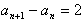
∴数列{an}是以3为首项,以2为公差的等差数列,
∴an=3+2(n-1)=2n+1。
(2)∵
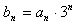
∴
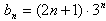
∴
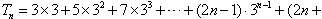 1)·3n ①
1)·3n ①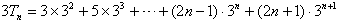 ②
②由①-②得
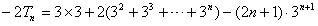
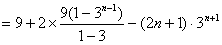
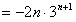
∴
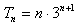 。
。
练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|