题目内容
函数 的奇偶性为________.
的奇偶性为________.
奇函数
分析:先求出f(x)的定义域,判断可得其定义域关于原点对称,再判断可得f(-x)=-f(x),即可得得到f(x)为奇函数.
解答:对于 ,有
,有 >0,解可得-1<x<1,
>0,解可得-1<x<1,
即函数f(x)的定义域为(-1,1),关于原点对称;
f(-x)=(-x)3+lg =-x3-lg
=-x3-lg =-f(x);
=-f(x);
则f(x)是奇函数;
故答案为奇函数.
点评:本题考查函数奇偶性的判断,注意要先求出函数的定义域,并判断其定义域是否关于原点对称.
分析:先求出f(x)的定义域,判断可得其定义域关于原点对称,再判断可得f(-x)=-f(x),即可得得到f(x)为奇函数.
解答:对于
 ,有
,有 >0,解可得-1<x<1,
>0,解可得-1<x<1,即函数f(x)的定义域为(-1,1),关于原点对称;
f(-x)=(-x)3+lg
 =-x3-lg
=-x3-lg =-f(x);
=-f(x);则f(x)是奇函数;
故答案为奇函数.
点评:本题考查函数奇偶性的判断,注意要先求出函数的定义域,并判断其定义域是否关于原点对称.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
 的奇偶性为 .
的奇偶性为 . 的奇偶性为 .
的奇偶性为 . ,
, ,定义:
,定义:
 ,例如:
,例如: =(-5)(-4)(-3)(-2)(-1) =-120,则函数
=(-5)(-4)(-3)(-2)(-1) =-120,则函数 的奇偶性为( )
的奇偶性为( )
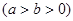 ,直线
,直线 交双曲线于A、B两点,
交双曲线于A、B两点, 的面积为S(O为原点),则函数
的面积为S(O为原点),则函数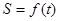 的奇偶性为 (
)
的奇偶性为 (
) 、
、 有关
有关 ,定义
,定义 ,如
,如 ,
, 的奇偶性为
的奇偶性为