Question

复数z和w满足：zw＋2iz－2iw＋1＝0．

(1)若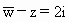，求z和w；

(2)求证：若|z|＝，则|w－4i|的值是一个常数，并求出这个常数．

Answer 1

答案：
解析：

解:(1)由，代入已知条件得－2iw＋1＝0，整理得．设w＝x＋yi(x，y∈R)代入上式得(x＋yi)(x－yi)－4i(x＋yi)＋2i(x－yi)＋5＝0，－2ix＋6y＋5＝0，即，因此解之得则w＝－i或w＝－5i，代入得z＝－i或3i，所以 　　(2)由已知，得，设w＝x＋yi(x，y∈R)得，整理得．∴|w－4i|＝即|w－4i|为一常数．

提示：

(1)利用关系式先代入减元，再设w＝x＋yi，把问题转化为实数问题；(2)根据模的意义，把条件转化为关于实数的关系式．