题目内容
已知抛物线![]() :
:![]() 与直线
与直线![]() :
:![]() 没有公共点,设点
没有公共点,设点![]() 为直线
为直线![]() 上的动点,过
上的动点,过![]() 作抛物线
作抛物线![]() 的两条切线,
的两条切线,![]() 为切点。
为切点。
(1)证明:直线![]() 恒过定点
恒过定点![]() ;
;
(2)若点![]() 与(1)中的定点
与(1)中的定点![]() 的连线交抛物线
的连线交抛物线![]() 于
于![]() 两点,证明:
两点,证明:![]() 。
。
(1)设![]() ,则
,则![]() 。由
。由![]() 得
得![]() ,所以
,所以![]() 。于是
。于是
抛物线![]() 在A点处的切线方程为
在A点处的切线方程为![]() ,即
,即![]() 。
。
设![]() ,则有
,则有![]() ,
,
设![]() ,同理有
,同理有![]() 。
。
所以AB的方程为![]() ,即
,即![]() ,所以直线AB恒过定点
,所以直线AB恒过定点![]() 。
。
(2)![]() 的方程为
的方程为![]() ,与抛物线方程
,与抛物线方程![]() 联立,消去
联立,消去![]() ,得
,得
![]() 。设
。设![]() ,
,![]() ,则
,则
![]() 、
、![]() ①。
①。
要证![]() ,只需证明
,只需证明![]() ,即
,即
![]() ②
②
由①知,②式左边![]()
![]() 。
。
故②式成立,从而结论成立。

练习册系列答案
相关题目
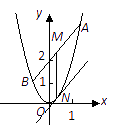 已知抛物线
已知抛物线 :
: 与直线
与直线 交于
交于 两点,
两点, 是线段
是线段 的中点,过
的中点,过 轴的垂线,垂足为
轴的垂线,垂足为 ,若
,若 ,则
,则 =
=
 :
: 与直线
与直线 相交于
相交于 ,
, 两点,以抛物线
两点,以抛物线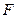 为圆心、
为圆心、 为半径(
为半径( 为坐标原点)作⊙
为坐标原点)作⊙ ,
, 相交于
相交于 ,
, 两点,则
两点,则 的值是
的值是