题目内容
在数列{an}中，对于任意的正整数n都有a1+a2+…+an=3n-1，则{an2}的前n项和为（ ）
分析：由a1+a2+a3+…+an=3n-1，可求得an，从而可知an2，再判断数列{an2}是等比数列，以及首项和公比，再利用等比数列的求和公式即可求得答案．
解答：解：∵a1+a2+a3+…+an=3n-1，①
∴a1+a2+a3+…+an+1=3n+1-1，②
②-①得：an+1=3n+1-3n=2×3n，
∴an=2×3n-1．
当n=1时，a1=31-1=2，符合上式，
∴an=2×3n-1．
∴an2=4×9n-1，∴a12=4，
∴{an2}是以4为首项，9为公比的等比数列，
∴a12+a22+a32+…+an2=
=
，
故选B．
∴a1+a2+a3+…+an+1=3n+1-1，②
②-①得：an+1=3n+1-3n=2×3n，
∴an=2×3n-1．
当n=1时，a1=31-1=2，符合上式，
∴an=2×3n-1．
∴an2=4×9n-1，∴a12=4，
∴{an2}是以4为首项，9为公比的等比数列，
∴a12+a22+a32+…+an2=
| 4(1-9n) |
| 1-9 |
| 9n-1 |
| 2 |
故选B．
点评：本题考查数列的求和，考查数列通项公式的确定及等比数列的判断与求和公式的综合应用，属于中档题．
练习册系列答案
课课优能力培优100分系列答案
优百分课时互动系列答案
相关题目
，都有
（k为常数），则称{an}为“等差比数列”. 下面对“等差比数列”的判断： ①k不可能为0；②等差数列一定是等差比数列；③等比数列一定是等差比数列；④通项公式为
的数列一定是等差比数列，其中正确的判断为（ ）
=k(k为常数)，则称数列{an}为“等差比数列”，下面对“等差比数列”判断：①k不可能为0；②等差数列一定是等差比数列；③等比数列一定是等差比数列；④通项公式为an=a·bn+c(a≠0，b≠0、1)的数列一定是等差比数列，其中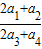判断正确的是
= ．