题目内容
(2012•宣城模拟)袋中装有2个白球,2个红球,它们大小、形状完全相同,仅强度不同,白球被击中1次破裂(成粉末),红球被击中2次破裂(被击中1次外形不改变).现随机击2次,设每次均击中一球,每球被击中的可能性相等,记ξ为袋中剩余球的个数.
(Ⅰ)求袋中恰好剩2个球的概率;
(Ⅱ)求ξ的分布列和数学期望.
(Ⅰ)求袋中恰好剩2个球的概率;
(Ⅱ)求ξ的分布列和数学期望.
分析:(Ⅰ)袋中恰好剩2个球,表示分别击中两个白球,故可求概率;
(Ⅱ)ξ的可能取值:2,3,4.袋中恰好剩3个球分三类:击中一白一红;击中一红一白;击中同一红球;从而可求ξ的分布列及数学期望.
(Ⅱ)ξ的可能取值:2,3,4.袋中恰好剩3个球分三类:击中一白一红;击中一红一白;击中同一红球;从而可求ξ的分布列及数学期望.
解答:解:(Ⅰ)袋中恰好剩2个球,表示分别击中两个白球,P(ξ=2)=
×
×
=
…(4分)
(Ⅱ)ξ的可能取值:2,3,4 …(5分)
袋中恰好剩3个球分三类:击中一白一红P1=
×
×
=
;
击中一红一白P2=
×
×
=
;击中同一红球P3=
×
×
=
∴P(ξ=3)=P1+P2+P3=
(8分)
P(ξ=4)=
×
×
=
…(10分)
ξ的分布列如下:
Eξ=2×
+3×
+4×
=
…(12分)
| C | 1 2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 6 |
(Ⅱ)ξ的可能取值:2,3,4 …(5分)
袋中恰好剩3个球分三类:击中一白一红P1=
| C | 1 2 |
| C | 1 2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 3 |
击中一红一白P2=
| C | 1 2 |
| C | 1 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| C | 1 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 8 |
∴P(ξ=3)=P1+P2+P3=
| 17 |
| 24 |
P(ξ=4)=
| C | 1 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 8 |
ξ的分布列如下:
| ξ | 2 | 3 | 4 | ||||||
| P |
|
|
|
| 1 |
| 6 |
| 17 |
| 24 |
| 1 |
| 8 |
| 71 |
| 24 |
点评:本题重点考查离散型随机变量的概率分布列及数学期望,解题的关键是确定ξ的可能取值,并明确其意义.

练习册系列答案
相关题目
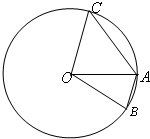 (2012•宣城模拟)如图,⊙O的半径为1,点A,B,C是⊙O上的点,且∠AOB=30°,AC=2AB,则
(2012•宣城模拟)如图,⊙O的半径为1,点A,B,C是⊙O上的点,且∠AOB=30°,AC=2AB,则